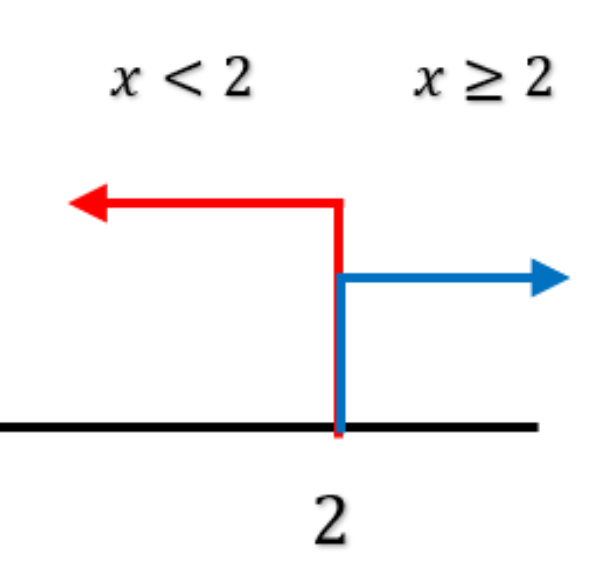
Bank Soal Matematika SMA Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Sains memiliki beberapa karakteristik, salah satunya adalah "sains merupakan kebenaran yang didasarkan pada data-data tanpa pengaruh pribadi". Pengertian tersebut merupakan arti dari karakteristik ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Biologi Sebagai Sains
Kelas X
Kurikulum 2013
K13
Rearrange the dialogue into a good one.
(1) George: Do you mean the ocean picture that I take?
(2) Alex: Absolutely! It was wonderful. Your photography skill is amazing.
(3) Alex: I saw your new post on Instagram!
(4) George: Thanks! I just captured it with my old camera.
The correct arrangement is ...
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting
Kelas X
Kurikulum 2013
K13
Bahasa Inggris
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
Kelas X
Kurikulum 2013
K13
Untuk mempercepat proses reaksi dalam suatu percobaan, terkadang perlu dilakukan pemanasan terhadap bahan tersebut. Pemanasan yang sering dilakukan adalah dengan menggunakan tabung reaksi. Cara pemanasan larutan dalam tabung reaksi yang benar adalah ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Kelas X
Kurikulum 2013
K13
EDIT: jawaban seharusnya adalah HP
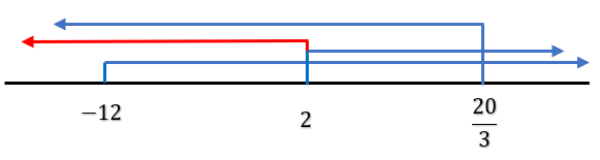
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak
Kelas X
Kurikulum 2013
K13
Matematika Wajib
Jumlah nilai x yang memenuhi sistem persamaan
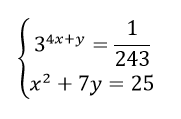
adalah....
Matematika
Level 10,10
Aljabar
Fungsi, Persamaan, dan Pertidaksamaan Eksponensial
Kurikulum Merdeka
KurMer
Kelas X
Kurikulum 2013
K13
Matematika Peminatan
Yang dimaksud dengan tuyang adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Kelas X
Kurikulum 2013
K13
Bahasa Indonesia
Perhatikan gambar berikut!
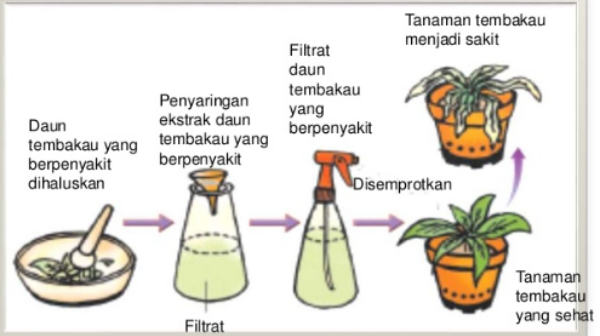
sumber: sucsload.blogspot.com
Penelitian pada tembakau seperti gambar di atas dilakukan oleh ....
Biologi
Level 10
Biologi
Virus
Sejarah Virus
Kelas X
Kurikulum 2013
K13
Fosfor di alam jumlahnya sangat banyak, tetapi tidak semuanya dapat terserap pada tumbuhan. Oleh karena itu, petani pada lahan pertanian memberikan asupan fosfor dalam bentuk ....
Biologi
Level 10
Biologi
Ekologi
Produktivitas dan Daur Biogeokimia
Kelas X
Kurikulum 2013
K13
Dalam pembuatan cubluk, hal yang harus diperhatikan adalah jarak cubluk dari galian sumur. Pertimbangan diambil untuk ....
Biologi
Level 10
Biologi
Perubahan dan Pelestarian Lingkungan Hidup
Bahan Pencemar dan Penanganan Limbah
Kelas X
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sains memiliki beberapa karakteristik, salah satunya adalah "sains merupakan kebenaran yang didasarkan pada data-data tanpa pengaruh pribadi". Pengertian tersebut merupakan arti dari karakteristik ....
Rearrange the dialogue into a good one.
(1) George: Do you mean the ocean picture that I take?
(2) Alex: Absolutely! It was wonderful. Your photography skill is amazing.
(3) Alex: I saw your new post on Instagram!
(4) George: Thanks! I just captured it with my old camera.
The correct arrangement is ...
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Untuk mempercepat proses reaksi dalam suatu percobaan, terkadang perlu dilakukan pemanasan terhadap bahan tersebut. Pemanasan yang sering dilakukan adalah dengan menggunakan tabung reaksi. Cara pemanasan larutan dalam tabung reaksi yang benar adalah ....
EDIT: jawaban seharusnya adalah HP
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Jumlah nilai x yang memenuhi sistem persamaan
adalah....
Yang dimaksud dengan tuyang adalah ….
Perhatikan gambar berikut!
sumber: sucsload.blogspot.com
Penelitian pada tembakau seperti gambar di atas dilakukan oleh ....
Fosfor di alam jumlahnya sangat banyak, tetapi tidak semuanya dapat terserap pada tumbuhan. Oleh karena itu, petani pada lahan pertanian memberikan asupan fosfor dalam bentuk ....
Dalam pembuatan cubluk, hal yang harus diperhatikan adalah jarak cubluk dari galian sumur. Pertimbangan diambil untuk ....