Diketahui:

$\tan\alpha=\frac{5}{12}$

$\tan\beta=\frac{7}{24}$

Ditanya:

$\sin\left(\alpha+\beta\right)=?$

Jawab:

Ingat kembali tentang konsep rasio trigonometri dan teorema Pythagoras.

Ilustrasikan sudut $\alpha$ dan sudut $\beta$

Sudut $\alpha$ dan sudut $\beta$ dapat diilustrasikan sebagai berikut.

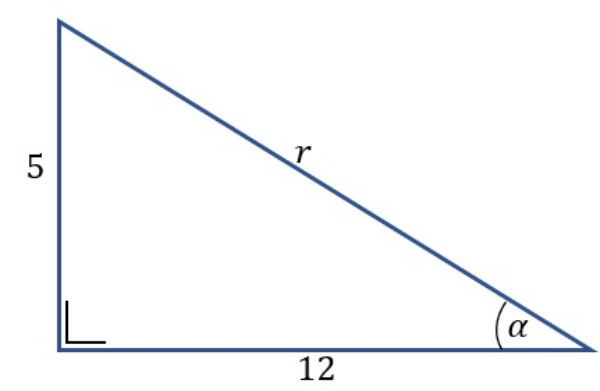
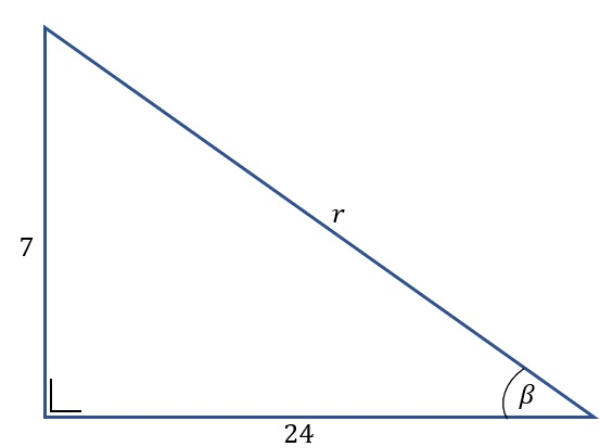
Mencari nilai $r$

$r_{\alpha}=\sqrt{5^2+12^2}$

$=\sqrt{25+144}$

$=\sqrt{169}$

$=13$

$r_{\beta}=\sqrt{7^2+24^2}$

$=\sqrt{49+576}$

$=\sqrt{625}$

$=25$

Mencari nilai sinus dan cosinus masing-masing sudut

$\sin\theta=\frac{\text{De}}{\text{Mi}}\$

$\cos\theta=\frac{\text{Sa }}{\text{Mi}}\ \$

Maka

$\sin\alpha=\frac{5}{13}$ dan $\cos\alpha=\frac{12}{13}$

$\sin\beta=\frac{7}{25}$ dan $\cos\beta=\frac{24}{25}$

Mencari nilai $\sin\left(\alpha+\beta\right)$

$\sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$

$=\frac{5}{13}\ .\ \frac{24}{25}+\frac{12}{13}\ .\ \frac{7}{25}$

$=\frac{1}{13}\ .\ \frac{24}{5}+\frac{12}{13}\ .\ \frac{7}{25}$

$=\frac{24}{65}+\frac{84}{325}$

$=\frac{24\left(5\right)+84}{325}$

$=\frac{120+84}{325}$

$=\frac{204}{325}$