Diketahui:

Tabung dan kerucut dengan alas berhimpit dan memiliki tinggi yang sama, diameter tabung adalah 14 cm, dan tinggi tabung adalah 18 cm.

Ditanya:

Volume tabung di luar kerucut?

Dijawab:

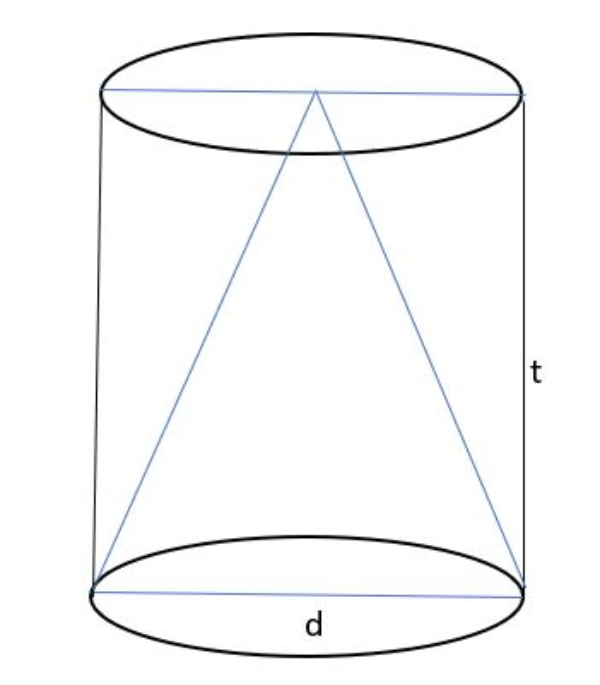
$V_T=\pi r^2t$,

di mana $V_T$ merupakan volume tabung, r merupakan jari-jari alas tabung, t merupakan tinggi tabung, dan $\pi\ =\frac{22}{7}$.

$\leftrightarrow\ V_T=\frac{22}{7}\times7^2\times18$

$\leftrightarrow\ V_T=\frac{22}{7}\times49\times18$

$\leftrightarrow\ V_T=2772$ cm$^3$.

$V_K\ =\frac{1}{3}\pi r^2t$,

di mana $V_K$ merupakan volume kerucut

$\leftrightarrow\ V_K=\frac{1}{3}\times\frac{22}{7}\times7^2\times18$

$\leftrightarrow\ V_K=\frac{1}{3}\times\frac{22}{7}\times49\times18$

$\leftrightarrow\ V_K=924$ cm$^3$.

Volume tabung di luar kerucut adalah

$V\ =V_T-V_K$

$\leftrightarrow\ V\ =2772-924$

$\leftrightarrow\ V\ =1848$ cm$^3$.

Jadi, volume tabung di luar kerucut adalah 1.848 cm$^3$.