Diketahui:

Volume kerucut = $V$ = 96$\pi$ liter (dm³) dan tinggi kerucut = $t$ = 8 dm.

Ditanya:

Luas permukaan kerucut = $L$ =?

Dijawab:

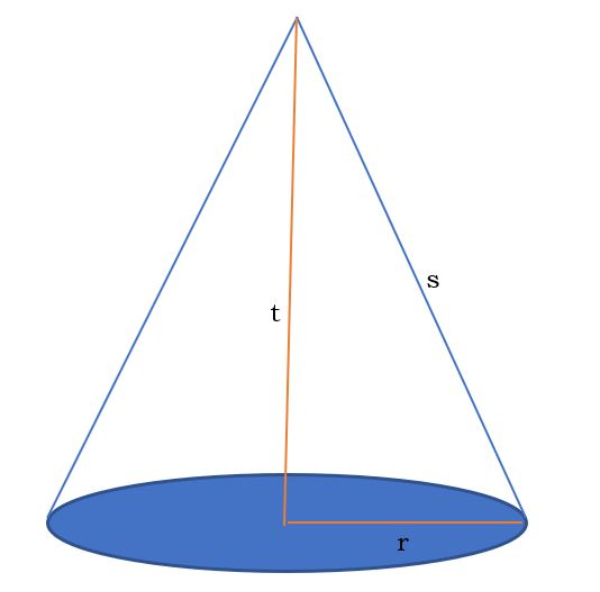
Volume kerucut:

$V=\frac{1}{3}\pi r^2t$

$\leftrightarrow96\pi=\frac{1}{3}\times\pi\times r^2\times8$

$\leftrightarrow96=\frac{1}{3}\times r^2\times8$

$\leftrightarrow r^2=\frac{96\times3}{8}$

$\leftrightarrow r^2=36$

$\leftrightarrow r=6$ dm.

Garis pelukis kerucut:

$s^2=r^2+t^2$

$\leftrightarrow s^2=6^2+8^2$

$\leftrightarrow s^2=36+64$

$\leftrightarrow s^2=100$

$\leftrightarrow s=10$ dm.

Luas permukaan kerucut:

$L=L_a+L_s$

$\leftrightarrow L=\pi r^2+\pi rs$

$\leftrightarrow L=\pi r\left(r+s\right)$

$\leftrightarrow L=\pi\times6\times\left(6+10\right)$

$\leftrightarrow L=\pi\times6\times16$

$\leftrightarrow L=96\pi$ dm².

Jadi, luas permukaan kerucut adalah 96$\pi$ dm².