Contoh Soal

Fungsi Kuadrat – Matematika SMP

Sampel materi untuk guru yang ingin cari soal latihan. Temukan bank soal lengkap dan update dengan cara mendaftar gratis. Kirim soal-soal ini ke murid di kelas Bapak/Ibu Guru lewat Google Classroom, dalam bentuk kuis online, tautan kuis, file kuis, atau cetak langsung!

Daftar

Pilih Kelas

Pilih Mata Pelajaran

Matematika Bahasa Indonesia IPA Bahasa Inggris IPS

Pilih Topik

Bilangan Berpangkat dan Bentuk Akar Persamaan Kuadrat Transformasi Geometri Kesebangunan dan Kongruen Bangun Ruang Sisi Lengkung Fungsi Kuadrat

Diberikan grafik fungsi kuadrat berikut.

Titik puncak fungsi tersebut adalah ....

A

✔

(2, $-$ 4)

B

( $-$ 4,2)

C

(4,0)

D

(0,4)

Pembahasan:

Titik puncak merupakan titik maksimum/minimum pada fungsi kuadrat. Diperhatikan kembali grafik berikut.

Jadi, titik puncaknya adalah (2, $-$ 4).

Diberikan grafik fungsi kuadrat berikut.

Titik potongnya terhadap sumbu-y adalah ....

A

✔

(0,0) saja

B

(4,0) saja

C

(0,0) dan (4,0)

D

(0,0) dan (0,4)

Pembahasan:

Titik potong terhadap sumbu-y adalah titik ketika x = 0. Diperhatikan kembali grafik berikut.

Jadi, titik potongnya terhadap sumbu-y adalah (0,0) saja.

Ingin coba latihan soal dengan kuis online?

Kejar Kuis

Diberikan grafik fungsi kuadrat berikut.

Titik potongnya terhadap sumbu-x adalah ....

A

✔

( $-$ 3,0) dan (1,0)

B

(0, $-$ 3) dan (0,1)

C

(3,0)

D

(0,3)

Pembahasan:

Titik potong terhadap sumbu-x adalah titik ketika y = 0. Diperhatikan kembali grafik berikut.

Jadi, titik potongnya terhadap sumbu-x adalah ( $-$ 3,0) dan (1,0).

Diberikan grafik fungsi kuadrat berikut.

Titik puncak fungsi tersebut adalah ....

A

(4, $-$ 1)

B

✔

( $-$ 1,4)

C

(1,0)

D

(0,1)

Pembahasan:

Titik puncak merupakan titik maksimum/minimum pada fungsi kuadrat. Diperhatikan kembali grafik berikut.

Jadi, titik puncaknya adalah ( $-$ 1,4).

Ingin cari soal-soal HOTS?

Soal HOTS

Persamaan grafik pada gambar di bawah ini adalah ....

A

✔

$y = x^{2} - 4 x$

B

$y = x^{2} + 4 x$

C

$y = - x^{2} - 4 x$

D

$y = 4 x^{2} - 2 x$

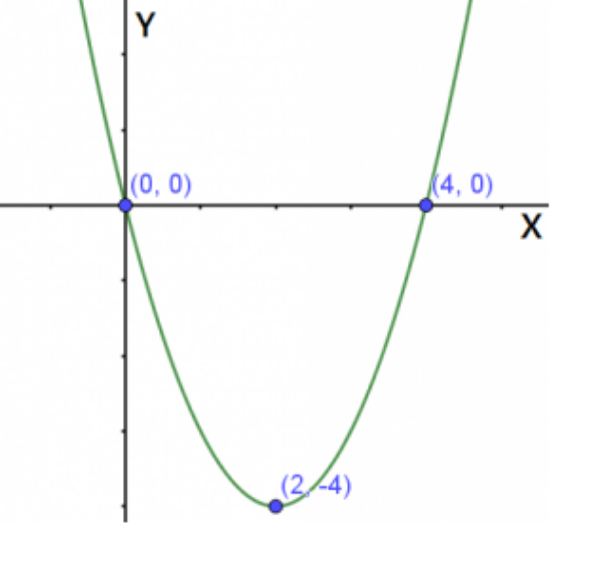
Pembahasan:

Alternatif Penyelesaian:

Ingat Rumus fungsi kuadrat memotong sumbu $x$ yaitu :

$y=a\left(x-x_1\right)\left(x-x_2\right)$

Melalui $\left(0,0\right)$ dan $\left(4,0\right)$

Jadi :

$0=a\left(x-0\right)\left(x-4\right)$

$0=a\left(x^2-4x\right)$

-----------------------------

Substitusikan $x=2$ dan $y=-4$ (Lihat gambar pada titik puncak)

$y=a\ \left(x^2−4x\right)$

$-4=a\ \left(2^2−4.2\right)$

$-4=a\ \left(4−8\right)$

$-4=a\ \left(-4\right)$

$a=1$

Maka,

$y=a\ \left(x^2−4x\right)$

$y=1\ \left(x^2−4x\right)$

$y=x^2-4x$

Koordinat titik potong grafik fungsi kuadrat $y = 2 x^{2} - x - 3$ terhadap sumbu $y$ adalah...

A

✔

$(0, - 3)$

B

$(0, 3)$

C

$(- 3, 0)$

D

$(3, 0)$

Pembahasan:

Alternatif Penyelesaian:

Memotong sumbu $y$ berarti $x=0$

$y=2x^2-x-3$

$y=2.0-0-3$

$y=-3$

Sehingga koordinatnya adalah $\left(0,-3\right)$

Ingin cari soal-soal AKM?

Hubungi Kami

Ordinat titik potong grafik fungsi $y = (x - 3) (x + 2)$ terhadap sumbu $y$ adalah...

A

-2

B

-4

C

✔

-6

D

-8

Pembahasan:

Alternatif Penyelesaian:

Memotong sumbu $y$ berarti $x=0$

$y=(x-3)(x+2)$

$y=x^2-x-6$

$y=0^2-0-6$

$y=-6$

Sehingga ordinatnya adalah $-6$

Koordinat titik potong grafik fungsi kuadrat $y = 5 x^{2} - 4 x + 5$ terhadap sumbu $y$ adalah...

A

$(0, - 5)$

B

✔

$(0, 5)$

C

$(5, 0)$

D

$(- 5, 0)$

Pembahasan:

Alternatif Penyelesaian:

Memotong sumbu $y$ berarti $x=0$

$y=5x^2-4x+5$

$y=5.0^2-4.0+5$

$y=5$

Sehingga koordinatnya adalah $\left(0,5\right)$

Ingin tanya tutor?

Tanya Tutor

Perhatikan gambar grafik berikut.

Misalkan fungsi kuadratnya adalah f(x) = ax²+ bx + c dengan a $\neq =$ 0, dan D = b² $-$ 4ac, maka ....

A

a > 0

B

b = 0

C

✔

c < 0

D

D < 0

Pembahasan:

Koefisien a menentukan arah terbukanya parabola.

a > 0 $\Leftrightarrow$ parabola terbuka ke atas
a < 0 $\Leftrightarrow$ parabola terbuka ke bawah

Koefisien b menentukan posisi titik puncak.

ab < 0 $\Leftrightarrow$ titik puncak berada di sebelah kiri sumbu-y
b = 0 $\Leftrightarrow$ titik puncak berada di sumbu-y
ab > 0 $\Leftrightarrow$ titik puncak berada di sebelah kanan sumbu-y

Koefisien c menentukan posisi titik potong terhadap sumbu-y.

c < 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di bawah sumbu-x
c = 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di titik (0,0)
c > 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di atas sumbu-x

Nilai D menentukan jumlah titik potong terhadap sumbu-x.

D < 0 $\Leftrightarrow$ tidak ada titik potong terhadap sumbu-x
D = 0 $\Leftrightarrow$ terdapat satu titik potong terhadap sumbu-x
D > 0 $\Leftrightarrow$ terdapat dua titik potong terhadap sumbu-x

Diperhatikan kembali gambar grafik berikut.

parabola terbuka ke bawah $\Leftrightarrow$ a < 0

titik puncak berada di sebelah kiri sumbu-y $\Leftrightarrow$ ab < 0

titik potong terhadap sumbu-y berada di bawah sumbu-x $\Leftrightarrow$ c < 0

terdapat dua titik potong terhadap sumbu-x $\Leftrightarrow$ D > 0

Jadi, jawabannya adalah c < 0.

10.

Perhatikan gambar grafik berikut.

Misalkan fungsi kuadratnya adalah f(x) = ax²+ bx + c dengan a $\neq =$ 0, dan D = b² $-$ 4ac, maka ....

A

a < 0

B

ab > 0

C

c < 0

D

✔

D > 0

Pembahasan:

Koefisien a menentukan arah terbukanya parabola.

a > 0 $\Leftrightarrow$ parabola terbuka ke atas
a < 0 $\Leftrightarrow$ parabola terbuka ke bawah

Koefisien b menentukan posisi titik puncak.

ab < 0 $\Leftrightarrow$ titik puncak berada di sebelah kiri sumbu-y
b = 0 $\Leftrightarrow$ titik puncak berada di sumbu-y
ab > 0 $\Leftrightarrow$ titik puncak berada di sebelah kanan sumbu-y

Koefisien c menentukan posisi titik potong terhadap sumbu-y.

c < 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di bawah sumbu-x
c = 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di titik (0,0)
c > 0 $\Leftrightarrow$ titik potong terhadap sumbu-y berada di atas sumbu-x

Nilai D menentukan jumlah titik potong terhadap sumbu-x.

D < 0 $\Leftrightarrow$ tidak ada titik potong terhadap sumbu-x
D = 0 $\Leftrightarrow$ terdapat satu titik potong terhadap sumbu-x
D > 0 $\Leftrightarrow$ terdapat dua titik potong terhadap sumbu-x

Diperhatikan kembali gambar grafik berikut.

parabola terbuka ke atas $\Leftrightarrow$ a > 0

titik puncak berada di sebelah kiri sumbu-y $\Leftrightarrow$ ab < 0

titik potong terhadap sumbu-y berada di atas sumbu-x $\Leftrightarrow$ c > 0

terdapat dua titik potong terhadap sumbu-x $\Leftrightarrow$ D > 0

Jadi, jawabannya adalah D > 0.

Daftar dan dapatkan akses ke puluhan ribu soal lainnya!

Buat Akun Gratis