Contoh Soal

Pembahasan:

Persamaan Linear Dua Variabel (PLDV) adalah sebuah bentuk relasi sama dengan pada bentuk aljabar yang memiliki dua variabel dan keduanya berpangkat satu. Maka jawabannya adalah

$p+2q=28$

karena di persamaan ini terdapat 2 variabel yakni p dan q.

Pembahasan:

Penyelesaian :

SPLDV adalah suatu sistem persamaan atau bentuk relasi sama dengan dalam bentuk aljabar yang memiliki dua variabel dan berpangkat satu dan apabila digambarkan dalam sebuah grafik maka akan membentuk garis lurus. Dan karena hal ini lah maka persamaan ini di sebut dengan persamaan linier. Maka:

a. Merupakan PLDV karena terdapat variabel $x$ dan $y$

b. Merupakan PLDV karena terdapat variabel $a$ dan $b$

c. Merupakan PLDV karena terdapat variabel $x$ dan $y$

d. Bukan merupakan PLDV karena hanya terdapat variabel $p$

Pembahasan:

Metode eliminasi merupakan suatu cara menyelesaikan persamaan linear dengan cara menghilangkan salah satu variabel dari variabel yang ada.

Metode substitusi merupakan cara menyelesaikan persamaan linear dengan memasukan salah satu persamaan ke dalam persamaan yang lain.

Metode penelitian adalah langkah yang dimiliki dan dilakukan oleh peneliti dalam rangka untuk mengumpulkan informasi atau data serta melakukan investigasi pada data yang telah didapatkan tersebut.

Jadi, yang bukan metode penyelesaian dari SPLDV adalah metode penelitian.

Pembahasan:

Misalkan:

- beras = $x$

- gula = $y$

Maka pernyataan PLDV yang paling tepat adalah $$ 30$x$ + 10$y$ = Rp173.000,00

Pembahasan:

Misal :

$p$ $+$ $q$ $=$ 8 ... (1)

4$p$ $-$ $q$ $=$ 12 ... (2)

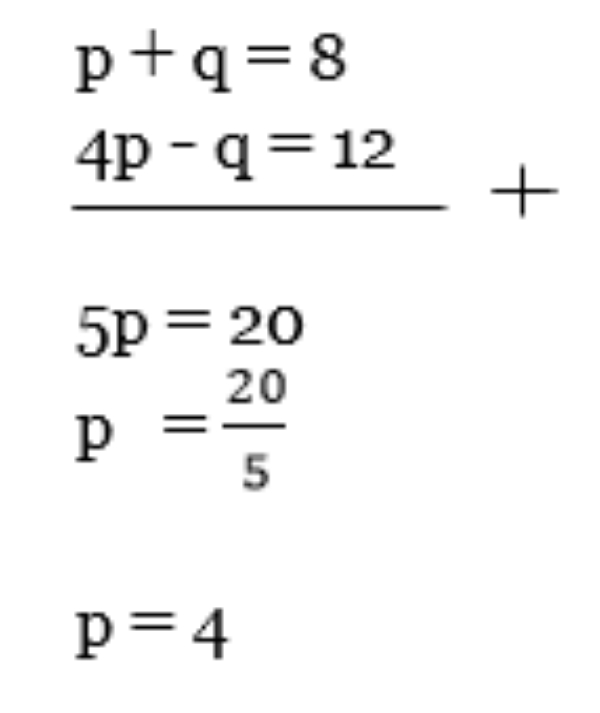
Subtitusikan $p$ $=$ 4 pada persamaan (1)

$p$ $+$ $q$ $=$ 8

4 $+$ $q$ $=$ 8

$q$ $=$ 8 $-$ 4

$q$ $=$ 4

Jadi

$p$ $-$ $q$ = 4 $-$ 4 $=$ 0

Pembahasan:

Diketahui :

• K $$ $$ $=40\ cm$
• K $=2p+2l$ ........(1)
• $l\ \ \ =p-2\ cm$ ....(2)

Ditanya :

• Luas karton $\left(L\right)$

Penyelesaian :

Subtitusikan nilai $l$ ke persamaan (1) :

K $=2p+2l$

40 cm $=2p+2\left(p-2\ cm\right)$

40 cm $=2p+2p-4\ cm$

40 cm $=4p-4\ cm$

$4p\ \ \ \ \ \ =40\ cm\ +\ 4\ cm$

$4p\ \ \ \ \ \ =44\ cm$

$p\ \ \ \ \ \ \ \ =\frac{44}{4}\ cm$

$p\ \ \ \ \ \ \ \ =11\ cm$

Subtitusikan nilai $p$ ke persamaan (2) :

$l\ \ \ \ \ \ \ \ =p-2\ cm$

$l\ \ \ \ \ \ \ \ =11\ cm-2\ cm$

$l\ \ \ \ \ \ \ \ =9\ cm$

Subtitusikan nilai $p$ dan $l$ ke dalam rumus Luas persegi panjang :

$L=p\times l$

$L=11\ cm\ \times9\ cm$

$L=99\ cm$ ²

Jadi, luas karton tersebut adalah 99 cm².

Pembahasan:

Jika nilai $q$ $=$ 4

Maka, diperoleh :

6$p$ $-$ 3$q$ $=$ 18

6$p$ $-$ 3 (4) $=$ 18

6$p$ $-$ 12 $=$ 18

6$p$ $=$ 18 $+$ 12

6$p$ $=$ 30

$p$ $=$ $\frac{30}{6}$

$p$ $=$ 5

Pembahasan:

Jika :

$x$ $=$ 0

Sehingga diperoleh :

5$x$ $+$ 3$y$ $-$ 15 $=$ 0

5 (0) $+$ 3$y$ $-$ 15 $=$ 0

0 $+$ 3$y$ $-$ 15 $=$ 0

3$y$ $=$ 15

$y$ $=$ $\frac{15}{3}$

$y$ $=$ 5

(0, 5)

Jika :

$y$ $=$ 0

Sehingga diperoleh :

5$x$ $+$ 3$y$ $-$ 15 $=$ 0

5$x$ $+$ 3 (0) $-$ 15 $=$ 0

5$x$ $+$ 0 $-$ 15 $=$ 0

5$x$ $-$ 15 $=$ 0

5$x$ $=$ 15

$x$ $=$ $\frac{15}{5}$

$x$ $=$ 3

(3, 0)

Jadi, koordinat titik potong sumbu $x$ dan sumbu $y$ dari persamaan 5$x$ $+$ 3$y$ $-$ 15 $=$ 0 adalah (0, 5) dan (3, 0)

Pembahasan:

Diketahui :

Kerbau dan bebek = 120 ekor

Kerbau (4 kaki) dan bebek (2 kaki) = 280 kaki

Ditanya :

Jumlah masing-masing kerbau dan bebek

Penyelesaian :

Misalkan : kerbau = $x$ , bebek = $y$

$\Rightarrow$ $x+y=120$

$y=120-x\$ ..........(1)

$\Rightarrow$ $4x+2y=280$ ................(2)

Subtitusikan persamaan (1) ke persamaan (2)

$4x+2y$ = 280

$4x+2\left(120-x\right)$ = 280

$4x+240-2x$ = 280

$2x$ = 280-240

$2x$ = 40

$x$ = 20

Subtitusikan nilai $x\$ ke persamaan (1) untuk mencari nilai $y$

$y=120-x\$

$y=120-20$

$y=100$

Jadi, di peternakan tersebut terdapat 20 ekor kerbau dan 100 ekor bebek

Pembahasan:

Penyelesaian :

Dari gambar di atas dapat dilihat bahwa garis tersebut memotong dua sumbu atau melalui dua titik, yaitu titik (0,6) dan titik (12,0). Jika titik (0,6) sebagai titik pertama dan (12,0) sebagai titik kedua, maka :

Gradien garis yang melalui titik (0,6) dan (12,0) adalah :

Persamaan garis yang melalui (0,6) dan memiliki gradien $-\frac{1}{2}$ adalah :

Jadi, persamaan linear dua variabel yang memenuhi grafik tersebut adalah persamaan garis linear, yaitu $x+2y=12$