Contoh Soal

Program Linear Dua Variabel – Matematika SMA

Sampel materi untuk guru yang ingin cari soal latihan. Temukan bank soal lengkap dan update dengan cara mendaftar gratis. Kirim soal-soal ini ke murid di kelas Bapak/Ibu Guru lewat Google Classroom, dalam bentuk kuis online, tautan kuis, file kuis, atau cetak langsung!

Daftar

Pilih Kelas

Pilih Mata Pelajaran

Matematika Bahasa Indonesia Bahasa Inggris Fisika Kimia Biologi Ekonomi Sosiologi Geografi Sejarah Indonesia Sejarah Peminatan

Pilih Topik

Induksi Matematika Program Linear Dua Variabel Matriks Transformasi Geometri Pola Bilangan Limit Fungsi Aljabar Turunan Fungsi Aljabar Integral Fungsi Aljabar Persamaan Trigonometri Faktorisasi Polinom Faktorisasi Polinom Jumlah dan Selisih Sin-Cos Lingkaran

Sepasang jam tangan laki-laki dan perempuan dijual dengan harga Rp500.000,-, tetapi jika membeli satuan dijual dengan harga Rp315.000,- baik jam untuk laki-laki maupun untuk perempuan. Setiap bulan, paling sedikit satu pasang jam tangan dapat terjual, sedangkan jam satuan tidak lebih dari 4 buah terjual. Jika jumlah jam terjual baik yang sepasang maupun satuan sebanyak-banyaknya 10 buah dan uang hasil penjualan sekurang-kurangnya Rp3.600.000,-, maka model matematika dalam sistem pertidaksamaan yang sesuai adalah ....

A

$x \geq 1; y \leq 4; x + y \leq 10;$ dan $315.000 x + 500.000 y \geq 3.600.000$

B

✔

$x \geq 1; y \leq 4; x + y \leq 10;$ dan $500.000 x + 315.000 y \geq 3.600.000$

C

$x \geq 1; y \leq 4; x + y \geq 10;$ dan $500.000 x + 315.000 y \leq 3.600.000$

D

$x \geq 1; y \leq 4; x + y \geq 10;$ dan $500.000 x + 315.000 y \geq 3.600.000$

E

$x \geq 1; y \leq 4; x + y \geq 10;$ dan $500.000 x - 315.000 y \geq 3.600.000$

Pembahasan:

Jumlah jam tangan sepasang: $x$

Jumlah jam tangan satuan: $y$

1) Jumlah semua jam

Jumlah jam tangan sepasang terjual paling sedikit 1, sehingga dapat ditulis $x\ge1$ dan jam tangan satuan paling banyak terjual 4, sehingga menjadi $y\le4$ .

Total semua jam tangan yang terjual:

jam tangan sepasang $+$ jam tangan satuan $\le10$ jam tangan

$x+y\le10$

Tanda $\le$ menunjukkan bahwa jumlah jam tangan yang terjual paling banyak 10, sehingga pasti jumlahnya kurang dari atau sama dengan 10.

2) Uang penjualan

Total uang penjualan:

$\left(Rp500.000\right)\left(x\right)+\left(Rp315.000\right)\left(y\right)\ge Rp3.600.000,-$

$500.000x+315.000y\ge3.600.000$

Tanda $\ge$ menunjukkan bahwa jumlah uang dari hasil penjualan jam tangan minimal (sekurang-kurangnya) Rp3.600.000,- tiap bulan.

Jadi, model matematika dari kasus tersebut adalah $x\ge1;\ y\le4;\ x+y\le10;$ dan $500.000x+315.000y\ge3.600.000$

Nilai maksimum dari $F = 2 x + y$ pada daerah $2 x + y \leq 6; x + 3 y \geq - 6;$ dan $2 x - 3 y \geq 6$ adalah ....

A

-2

B

-6

C

D

✔

E

Pembahasan:

1) Mencari titik potong sumbu- $x$ dan sumbu- $y$ tiap pertidaksamaan

2) Gambar grafik dan menetukan titik-titik pojok

Koordinat di titik C

Mencari nilai $y$ menggunakan metode eliminasi. Pertidaksamaan yang dieliminasi adalah garis merah dengan biru karena kedua garis tersebut yang saling berpotongan di titik C.

Menentukan nilai $x$ menggunakan metode substitusi

$2x+y=6$ , di mana $y=-\frac{18}{5}$

$2x+\left(-\frac{18}{5}\right)=6$

$2x=6+\frac{18}{5}$

$2x=\frac{30+18}{5}=\frac{48}{5}$

$x=\frac{24}{5}$

Titik-titik pojoknya adalah:

$A=\left(3,\ 0\right)$

$B=\left(0,\ -2\right)$

$C=\left(\frac{24}{5},\ -\frac{18}{5}\right)$

3) Nilai Optimum

Jadi, nilai maksimum dari $F=2x+y$ adalah 6

Ingin coba latihan soal dengan kuis online?

Kejar Kuis

Perhatikan gambar berikut!

Hasil penyelesaian dari sistem pertidaksamaan yang ditunjukkan oleh daerah arsiran di atas adalah ....

A

✔

$3 x + 2 y < 12; 2 x + 3 y \geq 6; x \leq 0;$ dan $y \geq 0$

B

$3 x - 2 y < 12; 2 x + 3 y \geq 6; x \leq 0;$ dan $y \geq 0$

C

$3 x + 2 y \leq 6; 2 x + 3 y > 6; x \leq 0;$ dan $y \geq 0$

D

$3 x + 2 y \leq 12; 2 x + 3 y > 24; x \leq 0;$ dan $y \geq 0$

E

$3 x - 2 y \leq 12; 2 x + 3 y > 24; x \leq 0;$ dan $y \geq 0$

Pembahasan:

1) Meninjau garis merah

Garis merah pada grafik memotong sumbu- $x$ di (4, 0) dan memotong sumbu- di (0, 6). Untuk membuat persamaan garis kita dapat menggunakan $ax+by=c$ , dengan $a$ adalah titik di sumbu- $y$ dan $b$ adalah titik di sumbu- $x$ , kemudian $c=ab$ . Oleh karena itu, persamaan garisnya menjadi berikut.

$6x+4y=\left(6\right)\left(4\right)$

$6x+4y=24$

Kita sederhanakan menjadi:

$3x+2y=12$

Karena daerah yang diarsir di sebelah kiri garis dan garis putus-putus, maka persamaannya menjadi:

$3x+2y<12$

Agar lebih yakin, kita dapat membuktikan dengan menggunakan titik selidik sebagai berikut.

Uji sembarang titik yang ada di dalam daerah pertidaksamaan, misalkan melalui (1, 0): $3\left(1\right)+2\left(0\right)=3<12$ (benar)
Uji sembarang titik yang ada di luar daerah pertidaksamaan, misalkan melalui (5, 0): $3\left(5\right)+2\left(0\right)=15<12$ (salah)

2) Meninjau garis biru

Garis biru pada grafik memotong sumbu- $x$ di (3, 0) dan memotong sumbu- di (0, 2). Untuk membuat persamaan garis kita dapat menggunakan $ax+by=c$ , dengan $a$ adalah titik di sumbu- $y$ dan $b$ adalah titik di sumbu- $x$ , kemudian $c=ab$ . Oleh karena itu, persamaan garisnya menjadi berikut.

$2x+3y=\left(2\right)\left(3\right)$

$2x+3y=6$

Karena daerah yang diarsir di sebelah kanan garis dan garis penuh (tidak putus-putus), maka persamaannya menjadi:

$2x+3y\ge6$

Agar lebih yakin, kita dapat membuktikan dengan menggunakan titik selidik sebagai berikut.

Uji sembarang titik yang ada di dalam daerah pertidaksamaan, misalkan melalui (4, 0): $2\left(4\right)+3\left(0\right)=8\ge6$ (benar)
Uji sembarang titik yang ada di luar daerah pertidaksamaan, misalkan melalui (2,0): $2\left(2\right)+3\left(0\right)=4\ge6$ (salah)

3) Meninjau garis pada sumbu- $x$ dan sumbu- $y$

Daerah yang diarsir pada grafik adalah di atas sumbu- $x$ yang berarti $y\ge0$ dan di sebelah kiri sumbu- $y$ yang berarti $x\le0$

Jadi, pertidaksamaan yang tepat adalah $3x+2y<12;\ 2x+3y\ge6;\ x\le0;$ dan $y\ge0$

Nilai maksimum dari $F = 3 x + 5 y$ pada daerah $3 x - 5 y \geq - 15; 3 x + y \leq - 3; x \leq 0;$ dan $y \geq 0$ adalah ....

A

B

C

✔

D

-15

E

-3

Pembahasan:

1) Mencari titik potong sumbu- $x$ dan sumbu- $y$ tiap kendala

2) Gambar grafik dan menetukan titik-titik pojok

Koordinat di titik C

Mencari nilai $y$ menggunakan metode eliminasi.

Menentukan nilai $x$ menggunakan metode substitusi

$3x+y=-3$ , di mana $y=2$

$3x+2=-3$

$3x=-3-2=-5$

$x=-\frac{5}{3}$

Titik-titik pojoknya adalah:

$A=\left(-5,\ 0\right)$

$B=\left(-1,\ 0\right)$

$C=\left(-\frac{5}{3},\ 2\right)$

3) Nilai Optimum

Jadi, nilai maksimum dari $F=3x+5y$ adalah 5

Ingin cari soal-soal HOTS?

Soal HOTS

Seorang penjual sandal online tiap bulannya dapat menjual sandal tidak lebih dari 22 pcs. Sandal tanpa hak dia jual dengan harga Rp25.000,- dan sandal ber-hak dia jual dengan harga Rp35.000,-. Hasil penjualan yang dia peroleh tidak lebih dari Rp600.000,- tiap bulannya. Model matematika dari persoalan tersebut adalah ....

A

$x \geq 0; y \geq 0; x + y \leq 22;$ dan $25.000 x - 35.000 y \leq 600.000$

B

$x \geq 0; y \geq 0; x + y \leq 22;$ dan $25.000 x + 35.000 y \geq 600.000$

C

✔

$x \geq 0; y \geq 0; x + y \leq 22;$ dan $25.000 x + 35.000 y \leq 600.000$

D

$x \geq 0; y \geq 0; x + y \leq 22;$ dan $35.000 x + 25.000 y \leq 600.000$

E

$x \geq 0; y \geq 0; x + y \leq 22;$ dan $25.000 x + 25.000 y \geq 600.000$

Pembahasan:

Jumlah sandal tanpa hak: $x$

Jumlah sandal ber-hak: $y$

Harga sandal tanpa hak: $a$

Harga sandal ber-hak: $b$

1) Jumlah semua sandal

Jumlah sandal tanpa hak dan sandal ber-hak tidak mungkin bernilai negatif, sehingga dapat kita tulis menjadi: $x\ge0$ dan $y\ge0$ .

Total semua sandal:

sandal tanpa hak $+$ sandal ber-hak $\le22$ buah

$x+y\leq 22$

Tanda $\le$ menunjukkan bahwa jumlah sandal tidak melebihi total sandal yang dia jual, yaitu 22 buah.

2) Harga total sandal

Total harga:

$ax+by\leq Rp600.000,-$

$(Rp25.000,-)(x)+(Rp35.000,-)(y)\leq Rp600.000,-$

$25.000x+35.000y\le600.000$

Jadi, model matematika dari kasus tersebut adalah $x\ge0;\ y\ge0;\ x+y\le22;$ dan $25.000x+35.000y\le600.000$

Di kelas XI MIPA 2, rak sepatu laki-laki dan perempuan mereka pisahkan. Ukuran kedua rak berbeda dan masing-masing rak minimal 2 tingkat. Satu tingkat rak sepatu laki-laki mampu menampung 3 pasang sepatu, sedangkan rak sepatu perempuan dapat menampung 4 pasang sepatu. Jumlah tingkat kedua rak tidak kurang dari lima tingkat, sedangkan jumlah sepatu yang dapat memenuhi kedua rak tidak lebih dari 27 pasang sepatu. Bentuk sistem pertidaksamaan dari persoalan ini adalah ....

A

$x \geq 2; y \geq 2; x + y \leq 5;$ dan $3 x + 4 y \geq 27$

B

✔

$x \geq 2; y \geq 2; x + y \geq 5;$ dan $3 x + 4 y \leq 27$

C

$x \leq 2; y \geq 2; x + y \geq 5;$ dan $3 x + 4 y \leq 27$

D

$x \geq 2; y \leq 2; x + y \geq 5;$ dan $3 x + 4 y \geq 27$

E

$x \geq 0; y \geq 0; x + y \geq 5;$ dan $3 x + 4 y \leq 27$

Pembahasan:

Jumlah tingkat rak laki-laki: $x$

Jumlah tingkat rak perempuan: $y$

1) Jumlah semua tingkat rak

Masing-masing rak minimal 2 tingkat, sehingga dapat kita tulis menjadi: $x\ge2$ dan $y\ge2$ .

Jumlah tingkat kedua rak tidak kurang dari lima tingkat, maka total semua tingkat rak:

tingkat rak laki-laki $+$ tingkat rak perempuan $\ge5$ tingkat

$x+y\ge5$

2) Jumlah sepatu

Satu tingkat rak sepatu laki-laki menampung 3 pasang sepatu dan 4 pasang sepatu untuk rak sepatu perempuan, jumlah sepatu yang dapat ditampung tidak lebih dari 27 pasang sepatu, pertidaksamaannya menjadi:

$3x+4y\le27$

Jadi, model matematika dari kasus tersebut adalah $x\ge2;\ y\ge2;\ x+y\ge5;$ dan $3x+4y\le27$

Ingin cari soal-soal AKM?

Hubungi Kami

Diketahui suatu sistem pertidaksamaan $4 x + 3 y \leq 24$ ; $x - y \geq 6$ ; $x \geq 0$ ; dan $y \leq 0$ . Grafik yang menunjukkan himpunan penyelesaian dari sistem pertidaksamaan tersebut adalah ....

A

B

C

✔

D

E

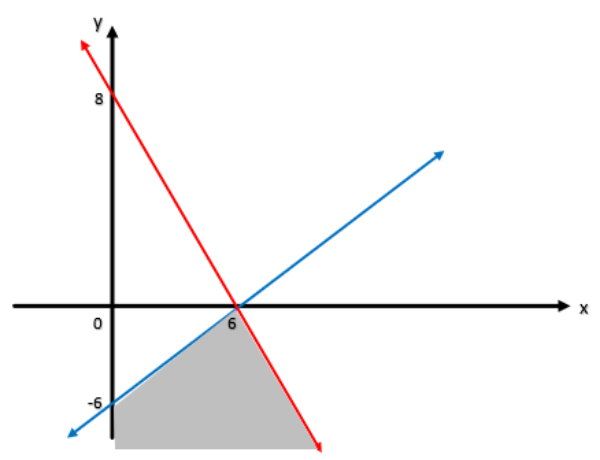
Pembahasan:

1) Titik potong garis $4x+3y\le24$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.

Untuk menentukan titik potong garis tersebut, kita dapat menentukan $x=0$ dan $y=0$

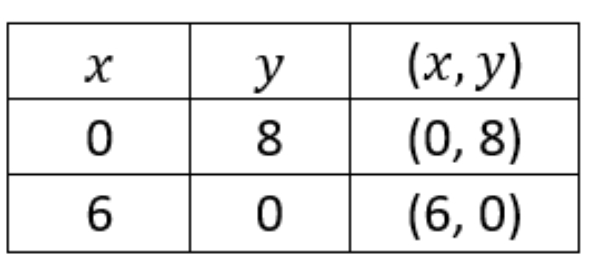
Dari tabel di atas kita tahu bahwa garis tersebut melalui titik (0, 8) dan (6, 0), kemudian karena pertidaksamaan bertanda $\le$ maka arsirannya di sebelah kiri.

2) Titik potong garis $x-y\ge6$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.

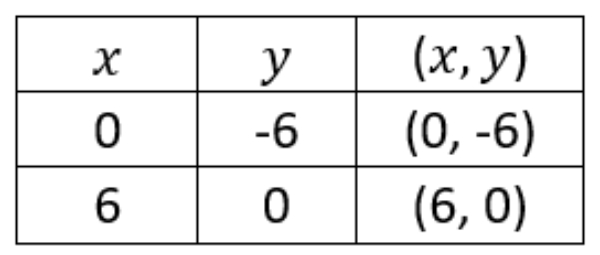
Dari tabel di atas kita tahu bahwa garis tersebut melalui titik (0, -6) dan (6, 0), kemudian karena pertidaksamaan bertanda $\ge$ maka arsirannya di sebelah kanan.

3) Titik potong garis $x\ge0$ , sehingga yang diarsir sebelah kanan, dan $y\le0$ maka arsirannya di bawah.

Untuk menguji, kita dapat menggunakan titik selidik yang dilingkupi daerah tersebut misalkan (0, -7)

$4x+3y\le24$

$4\left(0\right)+3\left(-7\right)\le24$

$-21\le24$ (benar)

$x-y\ge6$

$0-\left(-7\right)\ge6$

$7\ge6$ (benar)

Titik selidik di luar daerah tersebut misalkan (6, 5)

$4x+3y\le24$

$4\left(6\right)+3\left(5\right)\le24$

$39\le24$ (salah)

$x-y\ge6$

$6-\left(5\right)\ge6$

$1\ge6$ (salah)

Jadi, daerah penyelesaiannya menjadi:

Daerah penyelesaian dari bentuk pertidaksamaan linear $2 x + y \leq 6$ adalah ....

A

✔

B

C

D

E

Pembahasan:

Untuk menentukan titik potong suatu garis, kita dapat menggunakan cara substitusi $x=0$ dan $y=0$ ke persamaan garis yang ada

Titik potong garis $2x+y\le6$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.

Dari tabel di atas dapat diketahui bahwa:

garis tersebut melalui titik (0,6) dan (3,0),
pertidaksamaan bertanda $\le$ , maka arsirannya di sebelah kiri garis,
garis utuh (tidak putus-putus) karena menggunakan tanda pertidaksamaan $\le$ atau $\ge$

Jadi, daerah penyelesaian yang benar adalah:

Ingin tanya tutor?

Tanya Tutor

Nilai maksimum dari $f (x, y) = 4 x + y$ pada daerah $2 x + y \leq 8; 2 x - y \geq - 4; x \geq 0;$ dan $y \geq 0$ adalah ....

A

B

C

D

E

✔

Pembahasan:

1) Mencari titik potong sumbu- $x$ dan sumbu- $y$ tiap pertidaksamaan

2) Gambar grafik dan menentukan titik-titik pojok

Koordinat di titik C

Mencari nilai $y$ menggunakan metode eliminasi.

Menentukan nilai $x$ menggunakan metode substitusi

$2x+y=8$ , di mana $y=6$

$2x+6=8$

$2x=8-6=2$

$x=1$

Titik-titik pojoknya adalah:

$A=\left(0,\ 4\right)$

$B=\left(4,\ 0\right)$

$C=\left(1,\ 6\right)$

3) Nilai Optimum

Jadi, nilai maksimum dari $f\left(x,y\right)=4x+y$ adalah 16

10.

Diketahui sistem pertidaksamaan berikut.

Grafik yang terbentuk disajikan dalam gambar di bawah ini.

Daerah penyelesaian yang tepat adalah yang bernomor ....

A

✔

B

C

III

D

E

Pembahasan:

1) Titik potong garis $x-2y\le-10$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.

Untuk menentukan titik potong garis tersebut, kita dapat menentukan $x=0$ dan $y=0$ .

Dari tabel di atas kita tahu bahwa garis tersebut melalui titik (0, 5) dan (-10, 0), ditunjukkan oleh garis berwarna merah, kemudian karena pertidaksamaan bertanda $\le$ maka arsirannya di sebelah kiri, yaitu daerah I dan II.

2) Titik potong garis $4x+3y\ge-12$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.

Dari tabel di atas kita tahu bahwa garis tersebut melalui titik (0, -4) dan (-3, 0), ditunjukkan oleh garis berwarna biru, kemudian karena pertidaksamaan bertanda $\ge$ maka arsirannya di sebelah kanan, yaitu daerah I dan V.

3) Titik potong garis $x\le0$ dan $y\ge0$ , maka arsirannya di sebelah kiri dan atas, yaitu daerah I, II, III, dan V.

Oleh karena itu, daerah yang memenuhi ke empat syarat tersebut adalah nomor I, seperti ditunjukkan pada gambar berikut:

Agar lebih yakin, kita dapat membuktikan dengan menggunakan titik selidik sebagai berikut.

Uji sembarang titik yang ada di dalam daerah pertidaksamaan, misalkan melalui (0, 6): $0-2\left(6\right)=-12\le-10$ (benar)
Uji sembarang titik yang ada di luar daerah pertidaksamaan, misalkan melalui (-4, 0): $-4-2\left(6\right)=-4\le-10$ (salah)

Daftar dan dapatkan akses ke puluhan ribu soal lainnya!

Buat Akun Gratis