Pembahasan:
Diketahui:
Titik A(x,y) dirotasi terhadap titik pusat (−1,2) sebesar −90°
Bayangan yang dihasilkan adalah (6,−4)
Ditanya:
x−2y=?
Jawab:
Secara umum bayangan titik (x,y) yang dirotasikan pada pusat rotasi (a,b) dengan sudut rotasi θ adalah (x′,y′) dengan
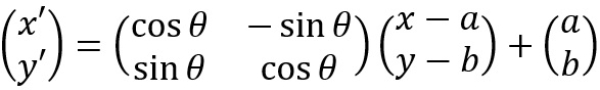
Diketahui titik A(x,y) dirotasi terhadap titik pusat (−1,2) sebesar −90°dan menghasilkan bayangan (6,−4) dengan a=−1,b=2,x′=6,y′=−4,θ=−90°
Sehingga diperoleh
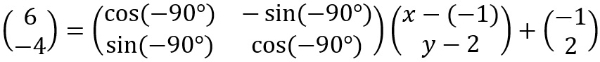
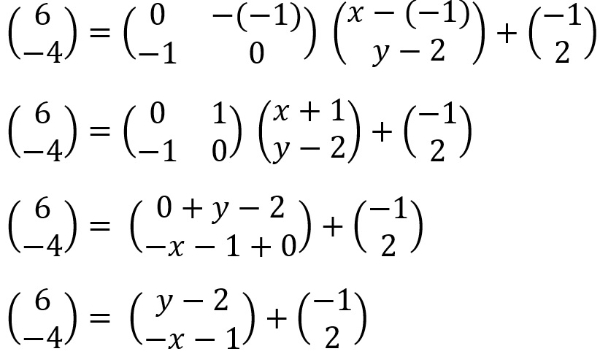
Artinya, 6=y−2+(−1) dan −4=−x−1+2
6=y−2+(−1)
6=y−2−1
y=9
−4=−x−1+2
x=5
Diperoleh
x−2y=5−2(9)
=5−18
=−13
Jadi, nilai x−2y=−13.
