Contoh Soal

Pembahasan:

Derajat merupakan pangkat tertinggi dari variabel yang terdapat pada suku banyak.

Untuk menentukannya, kita harus menjabarkan suku banyak terlebih dahulu.

$\left(x^2+2\right)^2\left(x+1\right)\left(x-7\right)^2$

$\Leftrightarrow\left(x^2+2\right)\left(x^2+2\right)\left(x+1\right)\left(x-7\right)\left(x-7\right)$

$\Leftrightarrow\left(x^4+4x^2+4\right)\left(x+1\right)\left(x^2-14x+49\right)$

$\Leftrightarrow\left(x^5+x^4+4x^3+4x^2+4x+4\right)\left(x^2-14x+49\right)$

$\Leftrightarrow\ x^7-13x^6+39x^5-3x^4+144x^3+144x^2+140x+196$

Pangkat tertinggi suku banyak tersebut adalah 7, sehingga suku banyak tersebut dapat dikatakan suku banyak berderajat 7.

Pembahasan:

Koefisien adalah bilangan real yang terletak di sebelah variabel.

Akan dicek pada setiap suku banyak yang ada.

Perhatikan suku banyak pertama!

$\Leftrightarrow\ 2x^2$ memiliki koefisien 2

Perhatikan suku banyak kedua!

$\Leftrightarrow\ x^3$ memiliki koefisien 1

Perhatikan suku banyak ketiga!

$\Leftrightarrow\ 5\sqrt{x^2}=5x^{ }$ memiliki koefisien 5

Perhatikan suku banyak keempat!

$\Leftrightarrow\ 10x^5$ memiliki koefisien 10

Perhatikan suku banyak kelima!

$\Leftrightarrow\sqrt{16x^4}=\sqrt{\left(4\right)^2x^4}=4x^2$ memiliki koefisien 4

Perhatikan suku banyak keenam!

$\Leftrightarrow-11=-11x^0$ memiliki koefisien -11

Jadi, koefisienurutan naiknya adalah $-11,5,2,4,1,10$

Pembahasan:

Akan dicek pada setiap suku banyak yang ada.

Perhatikan suku banyak pertama!

$\Leftrightarrow\ x=x^1$

Perhatikan suku banyak kedua!

$\Leftrightarrow\ -7=7x^0$

Perhatikan suku banyak ketiga!

$\Leftrightarrow\sqrt{x^8}=x^{\frac{8}{2}}=x^4$

Perhatikan suku banyak keempat!

$\Leftrightarrow\left(x^3\right)^2=x^6$

Perhatikan suku banyak kelima!

$\Leftrightarrow-5x^2$

Jadi, urutan turun dari $x-7+\sqrt{x^8}+\left(x^3\right)^2-5x^2$ dalah $\left(x^3\right)^2+\sqrt{x^8}-5x^2+x-7$

Pembahasan:

Derajat merupakan pangkat tertinggi dari variabel yang terdapat pada suku banyak.

Untuk menentukannya, kita harus menjabarkan suku banyak terlebih dahulu.

$\left(x^2-3\right)^2\left(1-2x+3x^2\right)$

$\Leftrightarrow\ \left(x^4-6x^2+9\right)\left(1-2x+3x^2\right)$

$\Leftrightarrow\ x^4-2x^5+3x^6-6x^2+12x^3-18x^4+9-18x+27x^2$

Kelompokkan suku yang sejenis

$\Leftrightarrow\ 3x^6-2x^5+x^4-18x^4+12x^3-6x^2+27x^2-18x+9$

$\Leftrightarrow\ 3x^6-2x^5-17x^4+12x^3+21x^2-18x+9$

Pangkat tertinggi penjabaran suku banyak adalah 6, sehingga derajat suku banyak tersebut adalah 6.

Pembahasan:

Diketahui:

$f\left(x\right)=2x^3+4x^2-5x-6=0$ dimana $a=2\ ,\ b=4\ ,\ c=-5\ \text{dan}\ d=-6$

Ditanya:

$\frac{x_1x_2x_3}{x_1+x_2+x_3}=?$

Jawab:

Gunakan teorema akar-akar $x_1+x_2+x_3=-\frac{b}{a}$

$\Leftrightarrow x_1+x_2+x_3=-\frac{b}{a}=-\frac{4}{2}=-2$

Gunakan teorema akar-akar $x_1x_2x_3=-\frac{d}{a}$

$\Leftrightarrow x_1x_2x_3=-\frac{d}{a}=-\frac{-6}{2}=3$

Jadi, nilai dari $\frac{x_1x_2x_3}{x_1+x_2+x_3}=-\frac{3}{2}$

Pembahasan:

$f\left(x\right)=mx^3+x^2+x+2$ dibagi $\left(3x-2\right)$ akan menghasilkan sisa 4, maka persamaan akan sama dengan 4.

$\Leftrightarrow f\left(x\right)=mx^3+x^2+x+2=4$

$\Leftrightarrow f\left(\frac{2}{3}\right)=\left(\frac{2}{3}\right)^3m+\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)+2=4$

$\Leftrightarrow m\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)+2=4$

$\Leftrightarrow\frac{8}{27}m+\frac{4}{9}+\frac{2}{3}+2=4$

$\Leftrightarrow\ \frac{8}{27}m=4-2-\frac{4}{9}-\frac{2}{3}$

$\Leftrightarrow\ \frac{8}{27}m=2-\frac{4}{9}-\frac{6}{9}$

$\Leftrightarrow\ \frac{8}{27}m=\frac{18}{9}-\frac{4}{9}-\frac{6}{9}$

$\Leftrightarrow\ \frac{8}{27}m=\frac{8}{9}$

$\Leftrightarrow m=\frac{8}{9}\times\frac{27}{8}=3$

Jadi, nilai $m$ adalah 3

Pembahasan:

Karena $f\left(x\right)\ \text{dan}\ g\left(x\right)$ memiliki sisa yang sama, maka $f\left(x\right)=g\left(x\right)$

$\Leftrightarrow x^3-12x^2+11x+3=x^4-kx^3+10x$

Pembagi adalah $\left(x+3\right)$ , maka substitusi nilai $x=-3$ ke dalam persamaan

$\Leftrightarrow\left(-3\right)^3-12\left(-3\right)^2+11\left(-3\right)+3=\left(-3\right)^4-k\left(-3\right)^3+10\left(-3\right)$

$\Leftrightarrow-27-12\left(9\right)-33+3=81-k\left(-27\right)+(-30)$

$\Leftrightarrow-27-108-33+3=81+27k-30$

$\Leftrightarrow-27-108-33+3+30-81=27k$

$\Leftrightarrow-216=27k$

$\Leftrightarrow k=-8$

Jadi, nilai $k$ adalah -8

Pembahasan:

Metode penjumlahan bersusun dapat dilihat seperti di bawah

Jadi, hasil penjumlahannya adalah $6x^5-3x^3-9x^2-2x-1$

Pembahasan:

Diketahui:

$\left(x-2\right)$ faktor dari $x^3+ax^2+bx+6$

$$$\left(x-3\right)$ faktor dari $x^3+ax^2+bx+6$

$x_1<x_2<x_3$

Ditanya:

$2x_1-x_2+x_3$ $=?$

Jawab:

Menggunakan teorema faktor

Misalkan $f\left(x\right)$ adalah suatu suku banyak dan $\left(x-a\right)$ adalah salah satu faktornya dan $x=a$ adalah salah satu akarnya, jika dan hanya jika $f\left(a\right)=0$.

Diketahui $\left(x-2\right)$ merupakan faktor dari $x^3+ax^2+bx+6$, maka

$x=2$

$f\left(2\right)=0$

$\Leftrightarrow\ \left(2\right)^3+a\left(2\right)^2+b\left(2\right)+6=0$

$\Leftrightarrow\ 8+a\left(4\right)+b\left(2\right)+6=0$

$\Leftrightarrow\ 4a+2b+14=0$

$\Leftrightarrow\ 4a+2b=-14$

$\Leftrightarrow\ 2a+b=-7$ ...(1)

Diketahui $\left(x-3\right)$ merupakan faktor dari $x^3+ax^2+bx+6,$ maka

$x=3$

$f\left(3\right)=0$

$\Leftrightarrow\ \left(3\right)^3+a\left(3\right)^2+b\left(3\right)+6=0$

$\Leftrightarrow\ 27+a\left(9\right)+b\left(3\right)+6=0$

$\Leftrightarrow\ 27+9a+3b+6=0$

$\Leftrightarrow\ 9a+3b+33=0$

$\Leftrightarrow\ 9a+3b=-33$

$\Leftrightarrow\ 3a+b=-11$ ...(2)

Eliminasi persamaan (1) dan (2)

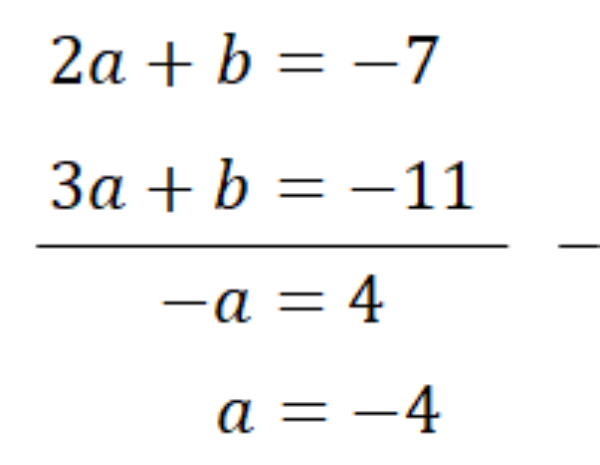
Substitusi $a=-4$ ke salah satu persamaan

$2a+b=-7$

$\Leftrightarrow\ 2\left(-4\right)+b=-7$

$\Leftrightarrow\ -8+b=-7$

$\Leftrightarrow\ b=-7+8$

$\Leftrightarrow\ b=1$

Sehingga bentuk polinomialnya menjadi:

$x^3-4x^2+x+6$ dengan faktor $\left(x-2\right)$ dan $\left(x-3\right)$

Bentuk Umum Polinomial adalah $f\left(x\right)=P\left(x\right)H\left(x\right)+S\left(x\right)$ dengan $P\left(x\right)$ adalah pembagi; $H\left(x\right)$ adalah hasil bagi; dan $S\left(x\right)$ adalah sisa pembagian.

$x^3-4x^2+x+6=\left(x-2\right)\left(x-3\right)H\left(x\right)+S\left(x\right)$

Karena $\left(x-2\right)$ dan $\left(x-3\right)$ merupakan faktor-faktor dari polinomial, maka polinomial habis dibagi oleh faktor-faktornya. Dengan kata lain, hasil pembagian tidak bersisa atau $S\left(x\right)=0$ sehingga

$x^3-4x^2+x+6=\left(x-2\right)\left(x-3\right)H\left(x\right)$

$x^3-4x^2+x+6=\left(x^2-5x+6\right)H\left(x\right)$

Untuk menemukan faktor ketiga, kita dapat memisalkan $H\left(x\right)=\left(x-k\right)$ sehingga

$x^3-4x^2+x+6=\left(x^2-5x+6\right)\left(x-k\right)$

$x^3-4x^2+x+6=x^3-kx^2-5x^2+5kx+6x-6k$

$x^3-4x^2+x+6=x^3+\left(-k-5\right)x^2+\left(5k+6\right)x-6k$

Menggunakan kesamaan suku banyak diperoleh

$-4=-k-5$

$\Leftrightarrow\ k=-5+4$

$\Leftrightarrow\ k=-1$

Sehingga faktor-faktornya adalah $\left(x-2\right),\ \left(x-3\right)$ dan $\left(x+1\right)$

$x-2=0\ \Leftrightarrow\ x=2$

$x-3=0\ \Leftrightarrow\ x=3$

$x+1=0\ \Leftrightarrow\ x=-1$

$x_1<x_2<x_3$ , maka

$x_1=-1,\ x_2=2,\ x_3=3$

$2x_1-x_2+x_3=2\left(-1\right)-2+3$

$\Leftrightarrow\ 2x_1-x_2+x_3=-2-2+3$

$\Leftrightarrow\ 2x_1-x_2+x_3=-1$

Jadi, nilai $2x_1-x_2+x_3$ adalah -1.

Pembahasan:

Diketahui:

$x^4-6x^3+mx^2+nx-8$

Dua akar pertama saling berlawanan: $x_1=-x_2\Leftrightarrow\ x_1+x_2=0$

Akar ketiga adalah dua kali akar keempat: $x_3=2x_4$

Ditanya:

$m=?$

$n=?$

Jawab:

Teorema akar-akar suku banyak.

Jika diketahui suatu suku banyak $ax^4+bx^3+cx^2+dx+e$, maka

$x_1+x_2+x_3+x_4=-\frac{b}{a}$

$x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4=\frac{c}{a}$

$x_1x_2x_3+x_1x_2x_4+x_1x_3x_4+x_2x_3x_4=-\frac{d}{a}$

$x_1x_2x_3x_4=\frac{e}{a}$

Diketahui suku banyak $x^4-6x^3+mx^2+nx-8$, maka

$a=1$

$b=-6$

$c=m$

$d=n$

$e=-8$

Diketahui $x_1+x_2=0$ dan $x_3=2x_4$, maka

$x_1+x_2+x_3+x_4=-\frac{b}{a}$

$\Leftrightarrow\ 0+2x_4+x_4=-\frac{\left(-6\right)}{1}$

$\Leftrightarrow\ 3x_4=6$

$\Leftrightarrow\ x_4=\frac{6}{3}$

$\Leftrightarrow\ x_4=2$

Sehingga diperoleh

$x_3=2x_4\ \Leftrightarrow\ x_3=4$

Kita dapat menentukan nilai $m$ dan $n$ dengan menggunakan akar-akar yang sudah diketahui.

Jika $f\left(x\right)=x^4-6x^3+mx^2+nx-8$ adalah suatu suku banyak dan $x_3=4$ adalah akar dari $f\left(x\right)$, maka $f\left(4\right)=0$ sehingga

$f\left(4\right)=0$

$\Leftrightarrow\ \left(4\right)^4-6\left(4\right)^3+m\left(4\right)^2+n\left(4\right)-8=0$

$\Leftrightarrow\ 256-6\left(64\right)+m\left(16\right)+4n-8=0$

$\Leftrightarrow\ 256-384+16m+4n-8=0$

$\Leftrightarrow\ -136+16m+4n=0$

$\Leftrightarrow\ 16m+4n=136$

$\Leftrightarrow\ 4m+n=34$ ...(1)

Jika $x_4=2$ adalah akar dari $f\left(x\right)$, maka $f\left(2\right)=0$ sehingga

$f\left(2\right)=0$

$\Leftrightarrow\ \left(2\right)^4-6\left(2\right)^3+m\left(2\right)^2+n\left(2\right)-8=0$

$\Leftrightarrow\ 16-6\left(8\right)+m\left(4\right)+2n-8=0$

$\Leftrightarrow\ 16-48+4m+2n-8=0$

$\Leftrightarrow\ -40+4m+2n=0$

$\Leftrightarrow\ 4m+2n=40$

$\Leftrightarrow\ 2m+n=20$ ...(2)

Eliminasikan persamaan (1) dan (2)

Substitusikan $m=7$ ke salah satu persamaan

$2m+n=20$

$\Leftrightarrow\ 2\left(7\right)+n=20$

$\Leftrightarrow\ 14+n=20$

$\Leftrightarrow\ n=20-14$

$\Leftrightarrow\ n=6$

Jadi, nilai $m$ dan $n$ berturut-turut adalah 7 dan 6.