Pembahasan:
Persoalan tersebut dapat diselesaikan berdasarkan definisi nilai mutlak, di mana untuk setiap bilangan real x, nilai mutlak ∣x∣ ditentukan oleh:
∣x∣=+x, untuk x>0
∣x∣=0, untuk x=0
∣x∣=−x, untuk x<0
x−∣2x−4∣+1≤17
Untuk menyelesaikan persamaan di atas, kita dapat menemukan interval masing-masing nilai mutlaknya sebagai berikut.
∣2x−4∣=2x−4 jika 2x−4≥0⇔2x≥4⇔x≥2
∣2x−4∣=−(2x−4)=−2x+4 jika 2x−4<0⇔2x<4⇔x<2
Sehingga diperoleh interval sebagai berikut.
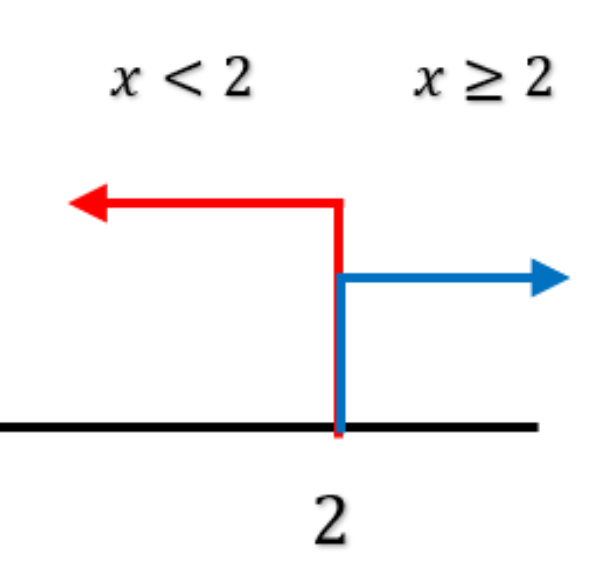
Selanjutnya kita dapat menemukan penyelesaian untuk masing-masing interval di atas.
Untuk x≥2 , bentuk pertidaksamaannya menjadi:
x−(2x−4)+1≤17
⇔x−(2x−4)≤17−1
⇔x−(2x−4)≤16
⇔x−2x+4≤16
⇔−x+4≤16
⇔−x≤16−4
⇔−x≤12 , kedua ruas dikali dengan −1 sehingga tanda pertidaksamaan berubah menjadi kebalikannya
⇔x≥−12
Untuk x<2, bentuk pertidaksamaannya menjadi:
x−(−(2x−4))+1≤17
⇔x−(−2x+4)≤17−1
⇔x+2x−4≤16
⇔3x−4 ≤16
⇔3x≤16+4
⇔3x≤20
⇔x≤320
Selanjutnya dapat digambarkan penyelesaiannya pada garis bilangan berikut.
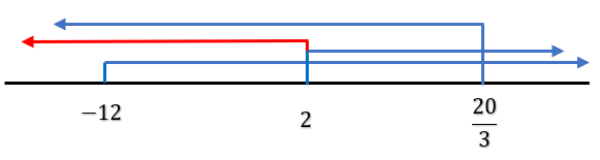
Jadi, HP ={x∣−12≤x≤320, x∈R}.
