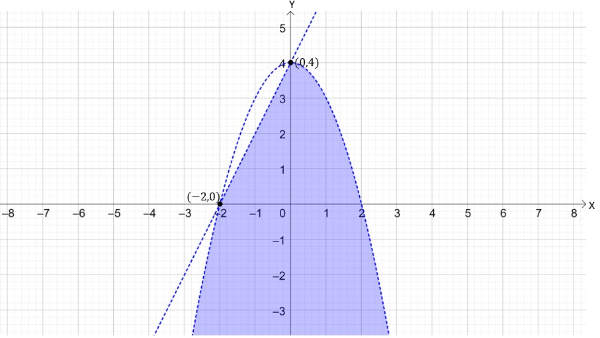
Pembahasan:
Langkah-langkah mencari daerah penyelesaian dari pertidaksamaan linear-kuadrat dua variabel adalah sebagai berikut.
Langkah pertama adalah melukis garis pembatas
Pada persoalan di atas, −4x+2y<8 adalah pertidaksamaan linear dan y<−x2+4 adalah pertidaksamaan kuadrat.
Garis pembatas pada sistem pertidaksamaan di atas adalah −4x+2y=8
Cara melukis garis pembatas dengan mencari titik potong garis dengan sumbu x dan sumbu y. Titik potong garis dengan sumbu koordinat dapat dinyatakan dalam tabel berikut.
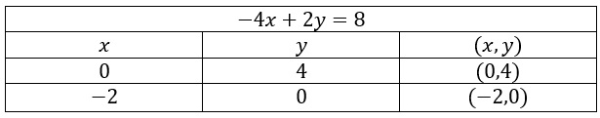
Selanjutnya, lukis garis pembatas dengan ketentuan:
Jika pertidaksamaan memuat tanda < atau > , maka garis pembatasnya digambar dengan garis putus-putus
Jika pertidaksamaan memuat tanda ≤ atau ≥ , maka garis pembatasnya digambar dengan garis penuh.
Pada pertidaksamaan −4x+2y<8 memuat tanda < sehingga garis pembatasnya berupa garis putus-putus.
Langkah kedua adalah melukis kurva pembatas
Kurva pembatas pada sistem pertidaksamaan di atas adalah y=−x2+4. Cara melukis kurva pembatas dengan mencari titik potong garis dengan sumbu x dan sumbu y. Titik potong kurva dengan sumbu koordinat dapat dinyatakan dalam tabel berikut.
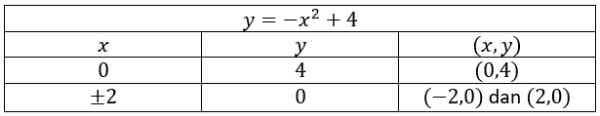
Titik puncak diperoleh dengan rumus x=−2ab dan y=−4aD dengan D=b2−4ac
Karena y=−x2+4 dengan a=−1,b=0,c=4 maka
x=−2(−1)0
x=20
x=0
y=−4(−1)02−4(−1)(4)
y=402+16
y=416
y=4
sehingga diperoleh titik puncak (0,4)
Pada pertidaksamaan y<−x2+4 memuat tanda < sehingga kurva pembatasnya berupa garis putus-putus.
Langkah ketiga adalah mencari titik potong garis dengan kurva
Mencari titik potong garis dengan kurva dapat dilakukan dengan melakukan substitusi persamaan −4x+2y=8 ke persamaan y=−x2+4
Terlebih dahulu ubah −4x+2y=8 ke bentuk eksplisit y=24x+8
y=−x2+4
24x+8=−x2+4
4x+8=−2x2+8
2x2+4x=0
x2+2x=0
x(x+2)=0
x=0 atau x=−2
Selanjutnya mencari nilai y
untuk x=0
y=−x2+4
y=−(0)2+4
y=0+4
y=4
sehingga diperoleh titik potong (0,4)
untuk x=−2
y=−x2+4
y=−(−2)2+4
y=−4+4
y=0
sehingga diperoleh titik potong (−2,0)
Langkah keempat adalah melukis daerah penyelesaian
Perhatikan tanda koefisien y dan tanda pertidaksamaan
Jika koefisien y atau y2 >0 maka bernilai positif (+)
Jika koefisien y tau y2 <0 maka bernilai negatif (−)
Jika tanda pertidaksamaan berupa > atau ≥ maka bernilai positif (+)
Jika tanda pertidaksamaan berupa < atau ≤ maka bernilai negatif (−)
Lakukan perkalian tanda koefisien dengan tanda pertidaksamaan
(+)×(+)=(+), maka diarsir di atas atau di luar pembatas
(−)×(−)=(+), maka diarsir di atas atau di luar pembatas
(+)×(−)=(−), maka diarsir di bawah atau di dalam pembatas
(−)×(+)=(−), maka diarsir di bawah atau di dalam pembatas
Dengan demikian,
Pada pertidaksamaan −4x+2y<8 koefisien y>0 dan tanda pertidaksamaan berupa < maka hasil kalinya
(+)×(−)=(−), maka diarsir di bawah garis pembatas
Pada pertidaksamaan y<−x2+4 koefisien y>0 dan tanda pertidaksamaan berupa < maka hasil kalinya
(+)×(−)=(−), maka diarsir di bawah kurva pembatas
Daerah penyelesaian sistem pertidaksamaan linear-kuadrat dua variabel merupakan irisan dari kedua daerah penyelesaian pertidaksamaan. Sehingga diperoleh daerah penyelesaian sebagai berikut.