Pembahasan:
Persoalan di atas dapat diselesaikan dengan metode eliminasi-substitusi. Langkah-langkah penyelesaian sistem persamaan linear tiga variabel menggunakan metode eliminasi-substitusi adalah sebagai berikut.
Sederhanakan bentuk sistem persamaan linear tiga variabel
Persamaan (1) dapat disederhanakan menjadi
a+2b=3(2c−3)
a+2b=6c−9
a+2b−6c=−9 ....(1)
Persamaan (2) dapat disederhanakan menjadi
2a−4b+5c=−7 ....(2)
Persamaan (3) dapat disederhanakan menjadi
6(2a+4c)=5(2b+2)
12a+24c=10b+10
12a−10b+24c=10
6a−5b+12c=5 ....(3)
Sehingga diperoleh sistem persamaan linear tiga variabel yang baru yaitu
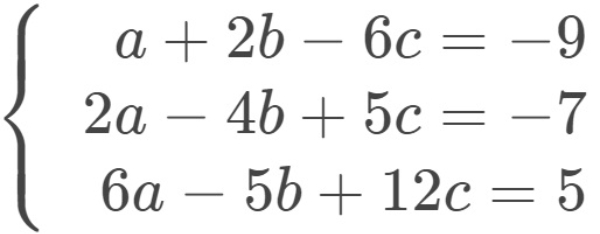
Eliminasikan salah satu variabel dari dua persamaan
Pilih persamaan (1) dan (2) untuk mengeliminasi variabel a sehingga diperoleh
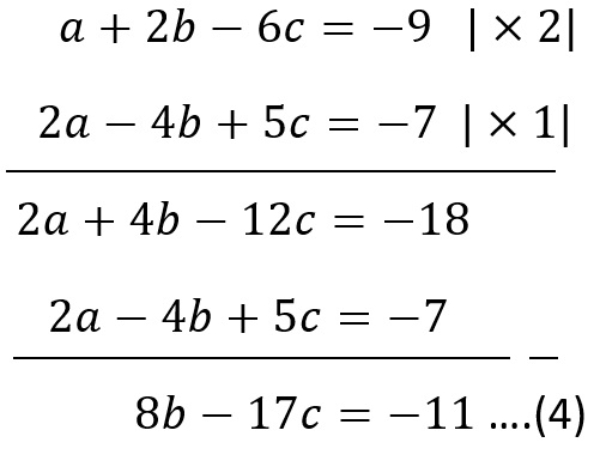
Pilih persamaan (1) dan (3) untuk mengeliminasi variabel a sehingga diperoleh
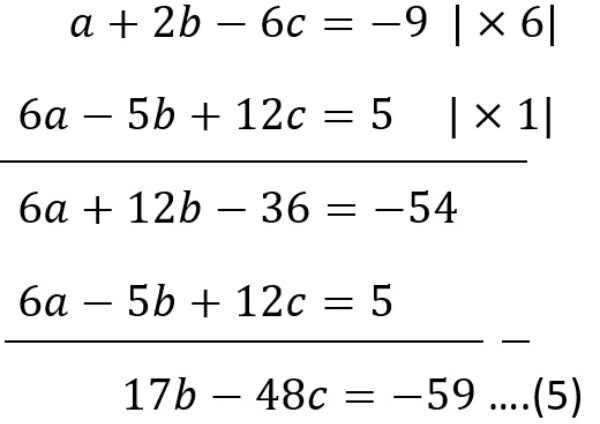
Selesaikan sistem persamaan linear dua variabel yang diperoleh
Diperoleh sistem persamaan linear dua variabel yaitu
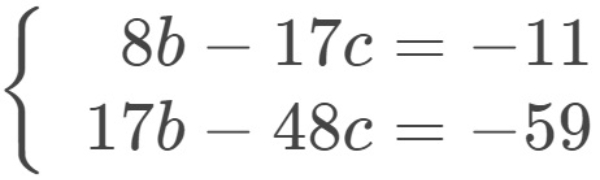
Selesaikan dengan metode eliminasi-substitusi
Proses eliminasi
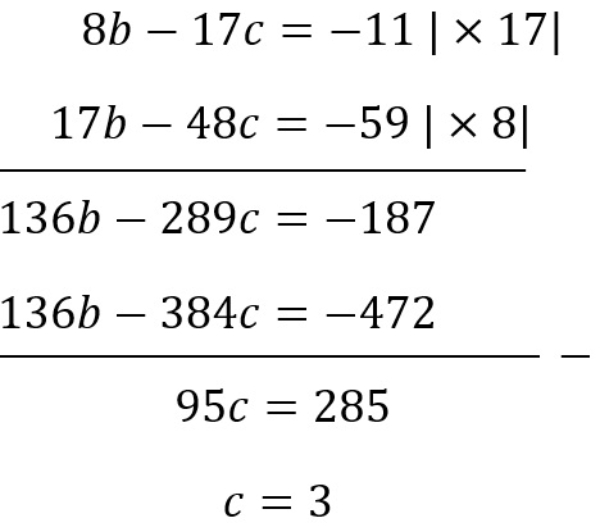
Proses substitusi
Substitusikan nilai c=3 ke persamaan (4)
8b−17c=−11
8b−17(3)=−11
8b−51=−11
8b=40
b=5
Substitusikan nilai b=5 dan c=3 ke persamaan (1)
a+2b−6c=−9
a+2(5)−6(3)=−9
a+10−18=−9
a−8=−9
a=−1
Periksa nilai penyelesaian
Pada persamaan (1)
a+2b−6c=−9
−1+2(5)−6(3)=−9
−1+10−18=−9
−9=−9 (benar)
Pada persamaan (2)
2a−4b+5c=−7
2(−1)−4(5)+5(3)=−7
−2−20+15=−7
−7=−7 (benar)
Pada persamaan (3)
6a−5b+12c=5
6(−1)−5(5)+12(3)=5
−6−25+36=5
5=5 (benar)
sehingga diperoleh penyelesaian a=−1, b=5, c=3 . Maka
HP={(−1,5,3)}
