Contoh Soal

Pembahasan:

Beberapa hal tentang dimensi diuraikan sebagai berikut.

• Dimensi digunakan untuk membuktikan dua besaran fisika setara atau tidak.
• Dua besaran atau lebih hanya dapat dijumlahkan atau dikurangkan jika besaran-besaran tersebut memiliki dimensi yang sama.
• Dimensi digunakan untuk menentukan persamaan yang pasti salah atau mungkin benar.
• Dimensi digunakan untuk menurunkan persamaan suatu besaran fisika jika kesebandingan besaran fisika tersebut terhadap besaran-besaran fisika lainnya diketahui.
• Jika kedua ruas memiliki dimensi yang sama, itu tidak berarti rumus tersebut benar. Hal ini dikarenakan mungkin terdapat suatu angka atau konstanta pada rumus yang tidak memiliki dimensi, misalnya $EK=\frac{1}{2}mv^2$, dengan nilai $\frac{1}{2}$ tidak dapat diperoleh dari analisis dimensi.

Kita tinjau masing-masing pernyataan

1. Dimensi digunakan untuk membuktikan dua besaran fisika setara atau tidak $\longrightarrow$ pernyataan benar
2. Dua besaran atau lebih dapat dijumlahkan atau dikurangkan jika besaran-besaran tersebut memiliki dimensi yang berbeda $\longrightarrow$ pernyataan salah
3. Dimensi digunakan untuk menentukan persamaan yang pasti salah atau mungkin benar $\longrightarrow$ pernyataan benar
4. Dimensi digunakan untuk menurunkan persamaan suatu besaran fisika jika kesebandingan besaran fisika tersebut terhadap besaran-besaran fisika lainnya diketahui $\longrightarrow$ pernyataan benar
5. Dalam menganalisis dimensi, jika kedua ruas memiliki dimensi yang sama, maka sudah pasti rumus tersebut benar $\longrightarrow$ pernyataan salah

Jadi, pernyataan yang salah adalah 2 dan 5

Pembahasan:

Aturan angka penting di antaranya adalah:

1) Semua angka bukan nol yang diperoleh dari hasil pengukuran termasuk angka penting

2) Angka nol yang terletak di antara dua angka bukan nol adalah angka penting

3) Semua angka nol yang terletak pada deretan akhir dari angka-angka yang ditulis di belakang koma desimal adalah angka penting

4) Angka-angka nol yang digunakan hanya untuk tempat titik desimal adalah bukan angka penting

5) Bilangan-bilangan puluhan, ratusan, ribuan, dan seterusnya yang memiliki angka-angka nol pada deretan akhir harus dituliskan dalam notasi ilmiah agar jelas apakah angka-angka nol tersebut termasuk angka penting atau bukan. Sebagai alternatif, dapat juga digunakan garis di bawah angka yang masih termasuk angka penting

Berdasarkan uraian di atas, dapat kita tinjau masing-masing jawaban sebagai beriku.

*0,0345; 450,1; $1,750\times10^4$; dan 16.000

0,0345 memiliki 3 angka penting, yaitu 3, 4, dan 5

*0,1004; 36,02; $1,800\times10^{-3}$; dan 17.500

Semua bilangan memiliki 4 angka penting

*0,1013; 4,020; $2,450\times10^{-6}$; dan 100.000

100.000 memiliki 5 angka penting, yaitu 1 dan keempat angka nol sampai yang diberi garis bawah

*0,04500; 72,130; $4,000\times10^{2}$; dan 20.100

72,130 memiliki 5 angka penting, yaitu semua angka adalah angka penting

*0,1500; 99,56; $1,2050\times10^{3}$; dan 27.100

$1,2050\times10^3$ memiliki 5 angka penting, yaitu semua angka adalah angka penting.

Jadi, bilangan yang memiliki 4 angka penting adalah 0,1004; 36,02; $1,800\times10^{-3}$; dan 17.500

Pembahasan:

Berhitung dengan angka penting memiliki beberapa aturan, yaitu:

1) Aturan pada penjumlahan dan pengurangan hasilnya hanya boleh mengandung satu angka taksiran.

2) Aturan pada perkalian dan pembagian hasil akhirnya hanya boleh mengandung angka penting sebanyak angka penting dari bilangan penting yang jumlah angka pentingnya paling sedikit.

Berdasarkan uraian di atas, dapat ditinjau masing-masing jawaban sebagai berikut.

*$1,24\ \text{cm}\times0,5\ \text{cm}=0,62\ \text{cm}^2$. Operasi perkalian, sehingga hasilnya harus memiliki 1 angka penting saja yaitu $0,6\ \text{cm}^2$

*$16,84\ \text{kg}:2,2\ \text{m}^3=7,654\ \text{kg/m}^3$. Operasi pembagian, sehingga hasilnya harus memiliki 2 angka penting yaitu $7,7\ \text{kg/m}^3$

*$0,213\ \text{m}+2,8\ \text{m}=3,013\ \text{m}$. Operasi penjumlahan, sehingga hasilnya harus mengandung satu angka taksiran yaitu $3,0\ \text{m}$

*$218,17\ \text{s}-120\ \text{s}=98\ \text{s}$. Operasi pengurangan, sehingga hasilnya harus mengandung satu angka taksiran, dan jawaban sudah benar

*$\left(1,2\ \text{m}\right)^2=1,44\ \text{m}^2$. Operasi perkalian, sehingga hasilnya harus memiliki 2 angka penting yaitu $1,4\ \text{m}^2$

Jadi, operasi hitung yang benar adalah $218,17\ \text{s}-120\ \text{s}=98\ \text{s}$

Pembahasan:

Diketahui:

Hasil laporan pengukuran panjang dengan mistar $L=\left(6,55\pm0,05\right)\ \text{cm}$

Ditanyakan:

Arti pengukuran panjang yang ditulis dalam laporan?

Jawab:

Hasil pengukuran suatu besaran dilaporkan sebagai berikut.

$x=x$₀ $\pm\Delta x$

pada soal dituliskan $L=\left(6,55\pm0,05\right)\ \text{cm}$, artinya kita tidak tahu nilai benar $x$₀. Tetapi, setelah diukur satu kali, maka $x$₀ berada di sekitar 6,55 cm, yaitu antara 6,50 cm (dari $6,55-0,05$) dan 6,60 cm (dari $6,55+0,05$).

Jadi, artinya adalah nilai $x$₀ berada di sekitar 6,55 cm.

Pembahasan:

Diketahui:

Jumlah buku $=75$

Tebal 1 buku $=3,85\ \text{cm}$

Ditanyakan:

Panjang rak satu deret?

Jawab:

Jumlah buku di sini merupakan bilangan eksak, sedangkan ukuran ketebalan buku adalah bilangan penting. Untuk mengetahui panjang rak, maka jumlah buku dikali dengan tebal satu buku.

Sesuai aturan angka penting, hasil perkalian atau pembagian antara bilangan penting dengan bilangan eksak hanya boleh memiliki angka penting sebanyak angka penting pada bilangan pentingnya.

Penyelesaiannya menjadi:

panjang rak $=75\times3,85\ \text{cm}$ (bilangan penting mengandung 3 angka penting)

$=288,75\ \text{cm}$ (lakukan pembulatan dengan aturan bahwa angka 5 atau lebih dibulatkan ke atas dan angka kurang dari 5 dibulatkan ke bawah)

$=289\ \text{cm}$ (ditulis dalam 3 angka penting)

Jadi, panjang raknya adalah $289\ \text{cm}$

Pembahasan:

Diketahui:

Jumlah warga $=180$

Jumlah beras $=750\ \text{kg}$

Ditanyakan:

Massa beras yang diterima tiap warga?

Jawab:

Jumlah warga di sini merupakan bilangan eksak, sedangkan jumlah beras adalah bilangan penting. Untuk mengetahui banyaknya beras yang diterima oleh tiap warga, maka jumlah beras dibagi dengan jumlah warga.

Sesuai aturan angka penting, hasil perkalian atau pembagian antara bilangan penting dengan bilangan eksak hanya boleh memiliki angka penting sebanyak angka penting pada bilangan pentingnya.

Penyelesaiannya menjadi:

massa beras tiap warga $=\frac{750}{180}$ (bilangan penting mengandung 2 angka penting)

$=4,167$

$=4,2$ (ditulis dalam 2 angka penting)

Jadi, massa beras yang diterima oleh tiap warga adalah 4,2 kg

Pembahasan:

Diketahui:

Luas penampang $A$

Panjang $l$

Beda kalor $\Delta T$

Laju perpindahan kalor $\frac{Q}{t}=\frac{kA\Delta T}{l}$

Ditanyakan:

Dimensi konduktivitas kalor?

Jawab:

Persamaan yang diketahui di soal adalah $\frac{Q}{t}=\frac{kA\Delta T}{l}$, sementara yang akan dicari adalah dimensi $k$, sehingga persamaannya menjadi $\frac{Ql}{tA\Delta T}=k$.

Laju perpindahan kalor $\frac{Q}{t}=\frac{kA\Delta T}{l}$, dengan $Q$ adalah energi kalor yang memiliki satuan joule, sama dengan satuan besaran energi yang lain, sehingga kita dapat menggunakan $Q=EK=\frac{1}{2}mv^2$, di mana $v=\frac{s}{t}$. Kemudian luas penampang $A=s^2$, dengan dimensi masing-masing besaran diuraikan sebagai berikut.

panjang $l$ memiliki satuan sama dengan jarak $s$, sehingga $\left[l\right]=\left[s\right]=\text{[L]}$

$\left[t\right]=\text{[T]}$

$\left[v\right]=\frac{\left[s\right]}{\left[t\right]}$ $\Leftrightarrow\frac{\text{[L]}}{\text{[T]}}=\text{[L][T]}^{-1}$

$\left[EK\right]=\frac{1}{2}\left[m\right]\left[v\right]^2$ $\Leftrightarrow\text{[M]}\left(\text{[L][T]}^{-1}\right)^2=\text{[M][L]}^2\text{[T]}^{-2}$

$\left[A\right]=\left[s\right]^2$ $\Leftrightarrow\left(\text{[L]}\right)^2=\text{[L]}^2$

$\left[\Delta T\right]=\left[T\right]=\ \text{[}\theta\text{]}$

maka, dimensi konduktivitas kalor menjadi:

$\left[k\right]=\frac{\left[Q\right]\left[l\right]}{\left[t\right]\left[A\right]\left[\Delta T\right]}$

$\frac{\left(\text{[M][L]}^2\text{[T]}^{-2}\right)\text{[L]}}{\text{[T]}\left(\text{[L]}^2\right)\text{[}\theta\text{]}}=\frac{\text{[M][L]}^3\text{[T]}^{-2}}{\text{[L]}^2\text{[T]}\text{[}\theta\text{]}}$

$=\frac{\text{[M][L]}^3\ \text{[L]}^{-2}\text{[T]}^{-2}\text{[T]}^{-1}}{\text{[}\theta\text{]}}$

$=\text{[M][L]}\text{[T]}^{-3}\text{[}\theta\text{]}^{-1}$

Jadi, dimensi konduktivitas kalor $k$ adalah $\text{[M][L]}\text{[T]}^{-3}\text{[}\theta\text{]}^{-1}$

Pembahasan:

Diketahui:

Jarak Bulan ke Bumi $=384.400.000\ \text{m}$

Ditanyakan:

Notasi ilmiah dan jumlah angka penting?

Jawab:

Aturan angka penting di antaranya adalah:

1) Semua angka bukan nol yang diperoleh dari hasil pengukuran termasuk angka penting

2) Angka nol yang terletak di antara dua angka bukan nol adalah angka penting

3) Semua angka nol yang terletak pada deretan akhir dari angka-angka yang ditulis di belakang koma desimal adalah angka penting

4) Angka-angka nol yang digunakan hanya untuk tempat titik desimal adalah bukan angka penting

5) Bilangan-bilangan puluhan, ratusan, ribuan, dan seterusnya yang memiliki angka-angka nol pada deretan akhir harus dituliskan dalam notasi ilmiah agar jelas apakah angka-angka nol tersebut termasuk angka penting atau bukan. Sebagai alternatif, dapat juga digunakan garis di bawah angka yang masih termasuk angka penting

Dalam notasi ilmiah, hasil pengukuran dinyatakan sebagai $a,...\ \times10^n$, dengan $a$ adalah bilangan asli dan $n$ adalah eksponen.

Untuk menuliskan notasi ilmiah dari $384.400.000\ \text{m}$, maka tanda koma digeser ke kiri melalui 8 angka, sehingga penulisannya menjadi $3,844\times10^8\ \text{m}$, dengan jumlah angka penting ada 4 angka penting.

Jadi notasi ilmiahnya adalah $3,844\times10^8\ \text{m}$ dan mengandung 4 angka penting.

Pembahasan:

Diketahui:

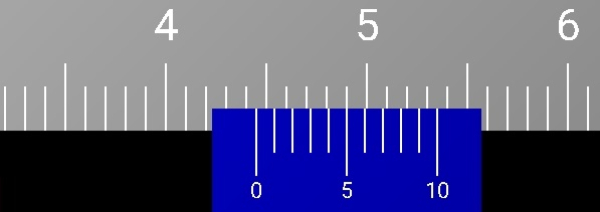
Gambar hasil pengukuran tinggi baterai menggunakan jangka sorong

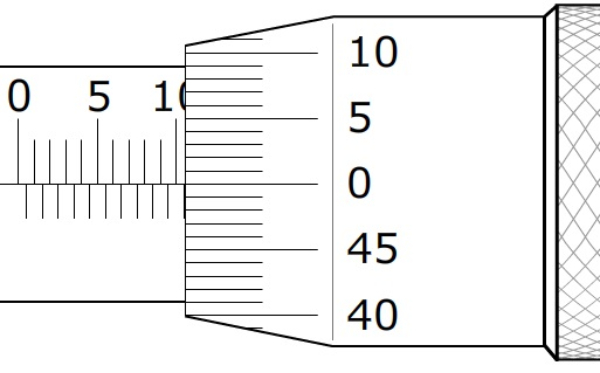
Gambar hasil pengukuran diameter baterai menggunakan mikrometer sekrup

Ditanyakan:

Volume baterai?

Jawab:

1) Menentukan tinggi baterai menggunakan jangka sorong

Jangka sorong merupakan alat ukur panjang yang memiliki ketelitian 0,1 mm atau 0,01 cm.

Terdapat dua jenis skala pada jangka sorong, yaitu skala utama yang bagian atas dan skala nonius yang bagian bawah. Satuan pada skala utama adalah cm, sedangkan nilai pada skala nonius ditunjukkan oleh angka yang terletak satu garis dengan skala utama kemudian angka tersebut dikali dengan 0,01 cm.

Pada gambar ditunjukkan:

skala utama $=4,4\ \text{cm}$

skala nonius $=5\times0,01\ \text{cm}=0,05\ \text{cm}$

tinggi baterai $=\text{skala utama }+\text{skala nonius}$

$=4,4\ \text{cm}+0,05\ \text{cm}$

$=4,45\ \text{cm}$

2) Menentukan diameter baterai menggunakan mikrometer sekrup

Mikrometer sekrup merupakan alat ukur panjang yang memiliki ketelitian 0,01 mm.

Terdapat dua jenis skala pada mikrometer sekrup, yaitu skala utama di bagian kiri dengan posisi horizontal dan skala nonius di bagian kanan dengan posisi vertikal. Satuan baik pada skala utama maupun skala nonius adalah mm, dengan nilai pada skala nonius ditunjukkan oleh angka yang terletak satu garis dengan garis utama kemudian angka tersebut dikali dengan 0,01 mm.

Pada gambar ditunjukkan:

skala utama $=10,5\ \text{mm}$

skala nonius $=0\times0,01\ \text{mm}=0$

diameter baterai $=\text{skala utama }+\text{skala nonius}$

$=10,5\ \text{mm}+0$

$=10,5\ \text{mm}$

3) Menentukan volume baterai

Bentuk baterai adalah silinder, sehingga $V=\frac{1}{4}\pi d^2t$

$V=\frac{1}{4}\left(\frac{22}{7}\right)\left(10,5\ \text{mm}\right)^2\left(4,45\ \text{cm}\right)$, samakan satuan kedalam mm semua

$=\frac{1}{4}\left(\frac{22}{7}\right)\left(10,5\right)\left(10,5\right)\left(44,5\right)$

$=\frac{1}{2}\left(11\right)\left(1,5\right)\left(10,5\right)\left(44,5\right)$

$=3.854,8125\ \text{mm}^3$

$=3,855\times10^3\ \text{mm}^3=3,855\ \text{cm}^3$

Jadi, volume baterai adalah $3,855\ \text{cm}^3$

Pembahasan:

Diketahui:

Besar massa $m$ $\left(1,24\pm0,06\right)\text{kg}$

Besar jarak $r$ $\left(3,2\pm0,3\right)\text{m}$

Besar momen inersia partikel $I=mr^2$

Ditanyakan:

Ketidakpastian relatif $\frac{\Delta I}{I_0}$ ?

Jawab:

Bentuk persamaan momen inersia adalah $I=mr^2$

Ketidakpastian untuk kasus perkalian dan eksponen dengan bentuk fungsi $z=ax^ny^m$ memiliki persamaan

$\frac{\Delta z}{z_0}=\left|n\right|\left|\frac{\Delta x}{x_0}\right|+\left|m\right|\left|\frac{\Delta y}{y_0}\right|$, dengan

$m=\left(m_0\pm\Delta m\right)$ $\Leftrightarrow m=\left(1,24\pm0,06\right)\text{kg}$

dan $r=\left(r_0\pm\Delta r\right)$ $\Leftrightarrow r=\left(3,2\pm0,3\right)\text{m}$

Penyelesaiannya menjadi:

$\frac{\Delta I}{I_0}=\left|n\right|\left|\frac{\Delta m}{m_0}\right|+\left|m\right|\left|\frac{\Delta r}{r_0}\right|$

$=\left|1\right|\left|\frac{0,06}{1,24}\right|+\left|2\right|\left|\frac{0,3}{3,2}\right|$

$=\left|0,048\right|+2\left|0,094\right|$

$=0,048+0,188=0,236$

ketidakpastian relatif $=\frac{\Delta z}{z_0}\times100\%$

$=0,236\times100\%=23,6\%$

Jadi, besar ketidakpastian relatif $\frac{\Delta I}{I_0}$ adalah 23,6%