Contoh Soal

Gaya Gravitasi – Fisika SMA

Sampel materi untuk guru yang ingin cari soal latihan. Temukan bank soal lengkap dan update dengan cara mendaftar gratis. Kirim soal-soal ini ke murid di kelas Bapak/Ibu Guru lewat Google Classroom, dalam bentuk kuis online, tautan kuis, file kuis, atau cetak langsung!

Daftar

Pilih Kelas

Kelas 1 Kelas 2 Kelas 3 Kelas 4 Kelas 5 Kelas 6 Kelas 7 Kelas 8 Kelas 9 Kelas 10 Kelas 11 Kelas 12

Pilih Mata Pelajaran

Matematika Bahasa Indonesia Bahasa Inggris Fisika Kimia Biologi Ekonomi Sosiologi Geografi Sejarah Indonesia Sejarah Peminatan

Pilih Topik

Hakikat Fisika dan Keselamatan Kerja Laboratorium Besaran Fisika dan Pengukurannya Gerak Lurus Vektor Gerak Parabola Gerak Melingkar Beraturan Dinamika Partikel Gaya Gravitasi Usaha dan Energi Impuls dan Momentum Linear Gerak Harmonik Sederhana
    1.

    Perhatikan besaran-besarann berikut ini.

    1. Massa planet Mars
    2. Massa satelit Mars
    3. Kuadrat jarak planet dan satelit
    4. Radius satelit Mars

    Besaran di atas yang mempengaruhi kuat medan gravitasi planet Mars pada satelitnya adalah ....

    A

    1 dan 2

    B
    ✔

    1 dan 3

    C

    1 dan 4

    D

    2 dan 3

    E

    2 dan 4

    Pembahasan:

    Persamaan kuat medan gravitasi adalah sebagai berikut

    g=GMr2g=\frac{GM}{r^2}

    dimana kuat medan gravitasi yang bekerja pada satelit Mars bergantung pada massa planet Mars dan jarak satelit dari planet Mars.

    Jadi, jawaban yang tepat adalah 1 dan 3.

    2.

    Sebuah satelit planet Mars yang sedang mengorbit dalam lintasan melingkar berpindah ke orbit lain yang jari-jarinya lebih kecil. Besaran berikut yang dimiliki satelit di mana nilainya akan tetap ketika berpindah adalah ....

    A

    gaya gravitasi

    B
    ✔

    sudut tempuh

    C

    percepatan gravitasi

    D

    kecepatan sudut

    E

    kecepatan tangensial

    Pembahasan:

    Gaya gravitasi, percepatan gravitasi, kecepatan sudut dan kecepatan tangensial adalah besaran-besaran yang terpengaruh oleh jarak objek ke planet. Ketika berpindah ke orbit yang jari-jarinya lebih kecil, maka gaya gravitasi, percepatan gravitasi, kecepatan sudut dan kecepatan tangensial akan semakin besar. Sedangkan sudut tempuh akan selalu sama yaitu 360o meskipun radius planet berubah-ubah.

    Ingin coba latihan soal dengan kuis online?

    Kejar Kuis
    3.

    Dua benda A dan B dengan massa masing-masing 2m dan m berada dalam posisi seperti terlihat pada gambar.

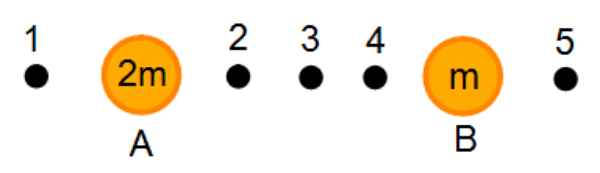
    Kemudian benda ke tiga akan diletakkan di sekitar benda A dan B. Letak benda ke tiga yang tepat agar memiliki total gaya gravitasi sama dengan nol adalah ....

    A

    posisi 1

    B

    posisi 2

    C

    posisi 3

    D
    ✔

    posisi 4

    E

    posisi 5

    Pembahasan:

    Agar total gaya gravitasi pada benda ke tiga sama dengan nol, maka kedua gaya yang bekerja harus memiliki tanda atau arah yang berlainan. Maka posisi yang mungkin ditempati benda ke tiga adalah posisi 2,3 dan 4.

    Letak yang paling tepat agar total gravitasi pada benda ke tiga sama dengan nol adalah benda tersebut harus diletakkan lebih dekat ke benda yang bermassa lebih kecil.

    Jadi, gaya gravitasi sama dengan nol jika benda ke tiga diletakkan pada posisi 4.

    4.

    Perhatikan pernyataan-pernyataan berikut.

    1. Sudut yang ditempuh lebih kecil
    2. Gerak planet semakin cepat
    3. Periode planet semakin cepat
    4. Area yag disapu lebih kecil pada periode yang sama

    Pernyataan yang tepat terkait gerak planet pada posisi di sekitar titik perihelium adalah ....

    A

    1 dan 2

    B

    1 dan 3

    C
    ✔

    2 dan 3

    D

    2 dan 4

    E

    3 dan 4

    Pembahasan:

    Titik perihelium adalah titik terdekat antara planet dan matahari. Titik perihelium ditunjukkan oleh titik P pada gambar berikut.

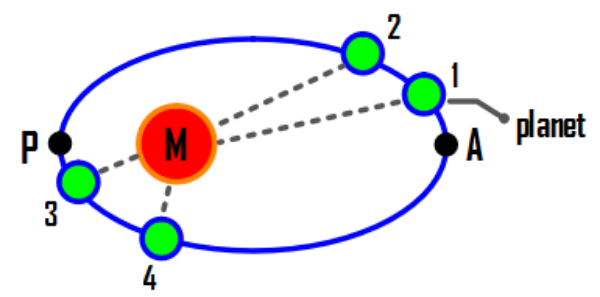
    Periode gerak planet dari titik 1 ke 2 sama dengan titik 3 ke 4. Sehingga, sudut yang ditempuh sekitar titik perihelium lebih besar. Begitu juga untuk kecepatan planet. Karena sudut yang ditempuh lebih besar dalam periode yang sama, maka kecepatan planet di sekitar titik perihelium juga lebih besar.

    Jika jarak yang ditempuh sama, maka periode planet di sekitar titik perihelium adalah lebih besar.

    Area yang disapu adalah sama jika periodenya juga sama berdasarkan hukum ke dua Kepler.

    Jadi, jawaban yang tepat berkaitan dengan gerak planet di sekitar titik perihelium adalah 2 dan 3.

    Ingin cari soal-soal HOTS?

    Soal HOTS
    5.

    Percepatan gravitasi pada permukaan planet adalah g. Jika suatu satelit berada pada jarak 2R dari pusat planet, maka percepatan gravitasi pada posisi ini adalah .... (R adalah jari-jari planet)

    A

    1/2 g

    B

    2 g

    C

    1/3 g

    D

    3 g

    E
    ✔

    1/4 g

    Pembahasan:

    Diketahui:

    Percepatan gravitasi di permukaan planet gP

    Jarak satelit dari pusat planet 2R

    Jari-jari planet R

    Ditanya:

    Percepatan gravitasi pada satelit gS = ?

    Jawaban:

    Percepatan gravitasi merupakan waktu rata-rata yang dibutuhkan partikel untuk menarik partikel lain ke arahnya dalam jarak atau medan gravitasi tertentu. Percepatan gravitasi pada satelit, dapat dihitung dengan persamaan berikut.

    gPgS=GMrP2GMrS2=rS2rP2=(2R)2R2=41\frac{g_P}{g_S}=\frac{\frac{GM}{r_P^2}}{\frac{GM}{r_S^2}}=\frac{r_S^2}{r_P^2}=\frac{\left(2R\right)^2}{R^2}=\frac{4}{1}

    Jadi, percepatan gravitasi pada satelit adalah gS=14gg_S=\frac{1}{4}g.

    6.

    Dimensi yang tepat untuk konstanta gravitasi (G) adalah ....

    A

    [M]−1[L]2[T]−2\left[M\right]^{-1}\left[L\right]^2\left[T\right]^{-2}

    B

    [M]−1[L]1[T]−2\left[M\right]^{-1}\left[L\right]^1\left[T\right]^{-2}

    C

    [M]−1[L]3[T]\left[M\right]^{-1}\left[L\right]^3\left[T\right]

    D
    ✔

    [M]−1[L]3[T]−2\left[M\right]^{-1}\left[L\right]^3\left[T\right]^{-2}

    E

    [M]−1[L]3[T]−1\left[M\right]^{-1}\left[L\right]^3\left[T\right]^{-1}

    Pembahasan:

    Gaya gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta yang terpisah sejauh rr. Persamaan gaya gravitasi adalah:

     F=GMmr2F=\frac{GMm}{r^2}

    Sehingga persamaan untuk konstanta gravitasi adalah

    G=Fr2MmG=\frac{Fr^2}{Mm}

    Untuk menentukan dimensi, dapat kita uraikan dari satuan masing-masing besaran.

    Gaya F=kgms2=[M][L][T]−2F=\frac{\text{kgm}}{\text{s}^2}=\left[M\right]\left[L\right]\left[T\right]^{-2}

    Jarak r2=m2=[L]2r^2=\text{m}^2=\left[L\right]^2

    Massa Mm=m2=kg2=[M]2Mm=m^2=\text{kg}^2=\left[M\right]^2

    Berdasarkan persamaan diatas, maka dimensi dari konstanta gravitasi adalah

    G=([M][L][T]−2)([L]2)[M]2=[M]−1[L]3[T]−2G=\frac{\left(\left[M\right]\left[L\right]\left[T\right]^{-2}\right)\left(\left[L\right]^2\right)}{\left[M\right]^2}=\left[M\right]^{-1}\left[L\right]^3\left[T\right]^{-2}

    Jadi, dimensinya adalah [M]−1[L]3[T]−2\left[M\right]^{-1}\left[L\right]^3\left[T\right]^{-2}

    Ingin cari soal-soal AKM?

    Hubungi Kami
    7.

    Dua buah benda bermassa 3m dan 2m berjarak 2r satu sama lain. Gaya gravitasi yang bekerja pada kedua benda tersebut adalah ....

    A

    14Gm2r2\frac{1}{4}\frac{Gm^2}{r^2}

    B

    12Gm2r2\frac{1}{2}\frac{Gm^2}{r^2}

    C

    Gm2r2\frac{Gm^2}{r^2}

    D
    ✔

    32Gm2r2\frac{3}{2}\frac{Gm^2}{r^2}

    E

    2Gm2r22\frac{Gm^2}{r^2}

    Pembahasan:

    Diketahui:

    Massa benda 1 M=3mM=3m

    Massa benda 2 m=2mm=2m

    Jarak dua benda r=2rr=2r

    Ditanya:

    Gaya gravitasi yang bekerja pada kedua benda F=?F=?

    Jawaban:

    Gaya gravitasi antara dua benda merupakan gaya tarik-menarik yang besarnya berbanding lurus dengan massa masing-masing benda dan berbanding terbalik dengan kuadrat jarak antara keduanya.

    Formula untuk mencari besar gaya gravitasi adalah

    F=GMmr2F=\frac{GMm}{r^2}, dimana M adalah massa bumi, m adalah massa bulan, r adalah jarak antara bumi bulan dan G adalah konstanta gravitasi umum.

    F=GMmr2=G(3m)(2m)(2r)2=6Gm24r2=32Gm2r2F=\frac{GMm}{r^2}=\frac{G\left(3m\right)\left(2m\right)}{\left(2r\right)^2}=\frac{6Gm^2}{4r^2}=\frac{3}{2}\frac{Gm^2}{r^2}

    Jadi, gaya gravitasi yang bekerja pada kedua benda tersebut adalah 32Gm2r2\frac{3}{2}\frac{Gm^2}{r^2}.

    8.

    Sebuah planet memiliki massa M dan menghasilkan potensial gravitasi V pada jarak R dari pusat planet. Jika R adalah jari-jari planet, maka potensial gravitasi pada titik yang berjarak 3R dari permukaan planet tersebut adalah ....

    A

    116V\frac{1}{16}V

    B

    8V8V

    C

    18V\frac{1}{8}V

    D

    4V4V

    E
    ✔

    14V\frac{1}{4}V

    Pembahasan:

    Diketahui:

    Massa planet M

    Potensial gravitasi V pada jarak R dari pusat planet

    Jari-jari planet R

    Jarak titik dari permukaan planet Rb=3RR_{\text{b}}=3R

    Ditanya:

    Potensial gravitasi pada titik yang berjarak 3R dari permukaan planet Vb=?V_{\text{b}}=?

    Jawaban:

    Potensial gravitasi suatu titik di dalam suatu medan gravitasi didefinisikan sebagai energi potensial gravitasi per satuan massa sebuah partikel uji kecil pada titik tersebut.

    V=EPgravm=−GMmrm=−GMrV=\frac{EP_{\text{grav}}}{m}=\frac{-\frac{GMm}{r}}{m}=\frac{-GM}{r}

    Tanda negatif menunjukkan bahwa untuk memindahkan benda dari posisi tertentu ke posisi lain yang jaraknya lebih jauh dari pusat planet diperlukan sejumlah energi.

    Titik yang berada pada jara 3R dari permukaan planet berarti berada pada jarak 4R dari pusat planet

    VVb=−GMR−GM4R=41\frac{V}{V_b}=\frac{-\frac{GM}{R}}{-\frac{GM}{4R}}=\frac{4}{1}

    Vb=14VV_b=\frac{1}{4}V

    Jadi potensial gravitasi pada titik yang berjarak 3R dari permukaan planet adalah 14V\frac{1}{4}V.

    Ingin tanya tutor?

    Tanya Tutor
    9.

    Dua buah satelit A dan B berjarak dari permukaan sebuah planet seperti gambar berikut.

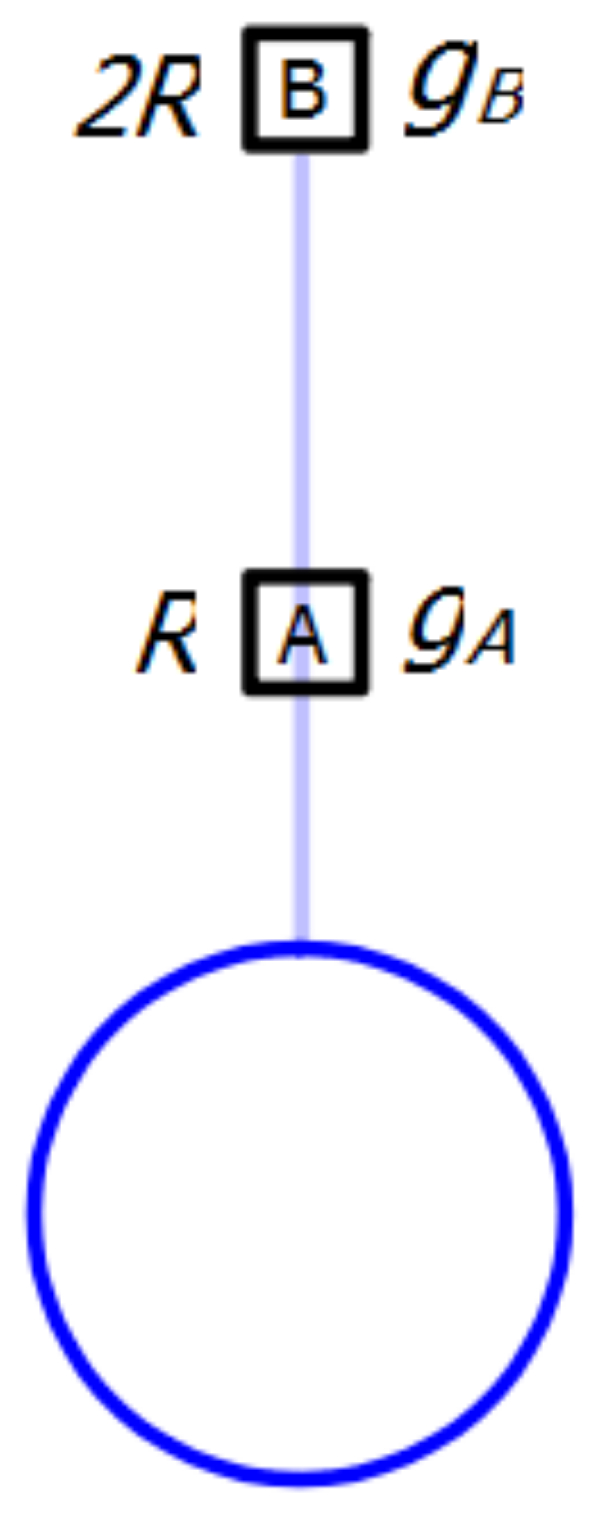
    Jika R adalah jari-jari planet, maka perbandingan percepatan gravitasi pada satelit A dan B adalah ....

    A

    2 : 3

    B

    3 : 2

    C

    4 : 9

    D
    ✔

    9 : 4

    E

    27 : 8

    Pembahasan:

    Diketahui:

    Jari-jari planet RR

    Jarak satelit A dari planet rA=Rr_A=R

    Jarak satelit B dari planet rB=2Rr_B=2R

    Ditanya:

    Perbandingan percepatan gravitasi pada satelit A dan B gA:gB=?g_A:g_B=?

    Jawaban:

    Percepatan gravitasi merupakan waktu rata-rata yang dibutuhkan partikel untuk menarik partikel lain ke arahnya dalam jarak atau medan gravitasi tertentu.

    Percepatan gravitasi pada satelit dihitung berdasarkan jaraknya dari pusat planet. Jika ditinjau dari pusat planet, maka jarak satelit-satelit tersebut adalah sebagai berikut.

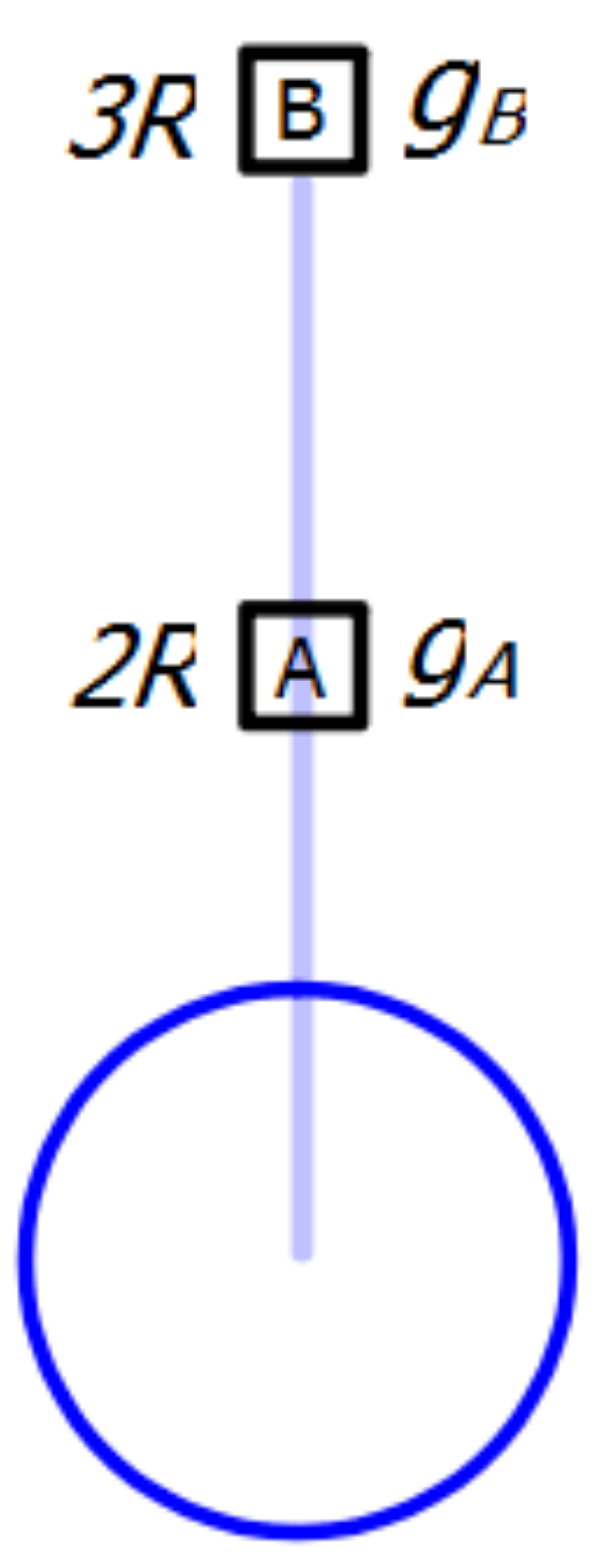
    Sehingga perbandingan percepatan gravitasi pada satelit A dan B adalah

    gAgB=GMrA2GMrB2=rB2rA2=(3R)2(2R)2=94\frac{g_A}{g_B}=\frac{\frac{GM}{r_A^2}}{\frac{GM}{r_B^2}}=\frac{r_B^2}{r_A^2}=\frac{\left(3R\right)^2}{\left(2R\right)^2}=\frac{9}{4}

    Jadi, perbandingan percepatan gravitasi pada satelit A dan B adalah 9 : 4.

    10.

    Sebuah benda A mengalami gaya gravitasi akibat dua benda lain di sampingnya seperti ditunjukkan oleh gambar.

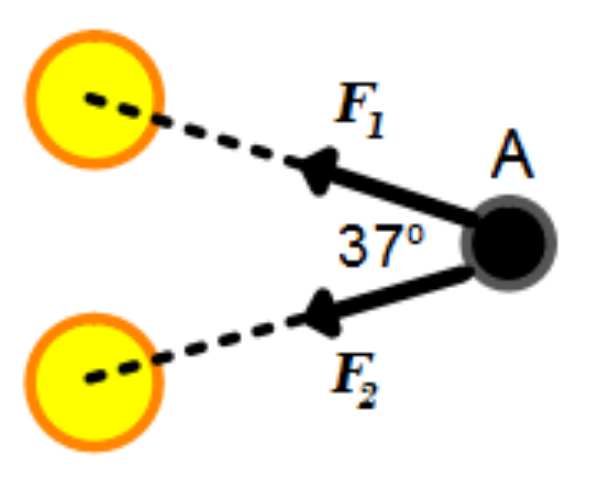
    Jika setiap gaya memiliki besar 10 N, maka gaya gravitasi total yang dialami benda A adalah ....

    A
    ✔

    610 N6\sqrt{10}\text{ N}

    B

    710 N7\sqrt{10}\text{ N}

    C

    810 N8\sqrt{10}\text{ N}

    D

    910 N9\sqrt{10}\text{ N}

    E

    1010 N10\sqrt{10}\text{ N}

    Pembahasan:

    Diketahui:

    Bekerja dua buah gaya F1=F2=F_1=F_2= 10 N

    Sudut di antara dua gaya θ=37o\theta=37^o

    Ditanya:

    Gaya gravitasi total R=?R=?

    Jawaban:

    Untuk kasus pada dua buah vektor gaya gravitasi yang membentuk sudut θ\theta, besar resultan gaya gravitasi dapat ditentukan dengan rumus kosinus sebagai berikut.

    R=F12+F22+2F1F2cos⁡θ=102+102+2(10)(10)cos⁡37oR=\sqrt{F_1^2+F_2^2+2F_1F_2\cos\theta}=\sqrt{10^2+10^2+2\left(10\right)\left(10\right)\cos37^o}

    =100+100+200(45)=360=610 N=\sqrt{100+100+200\left(\frac{4}{5}\right)}=\sqrt{360}=6\sqrt{10}\text{ N}

    Jadi, gaya gravitasi total yang bekerja pada benda A adalah 610 N6\sqrt{10}\text{ N}.

    Daftar dan dapatkan akses ke puluhan ribu soal lainnya!

    Buat Akun Gratis